
分析 利用二项式定理可知(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式中通项公式Tk,进而可确定展开式中常数项为T3,利用微积分基本定理化简可知a=2,代入计算即可.
解答 解:(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式中通项公式Tk=${C}_{6}^{k}$$(a\sqrt{x})^{6-k}$$(-\frac{1}{\sqrt{x}})^{k}$=(-1)ka6${C}_{6}^{k}$x3-k,
令x3-k=1,解得k=3,即展开式中常数项为T3=-20a6,
又∵a=${∫}_{0}^{π}$(sinx-1+2cos2$\frac{x}{2}$)dx
=${∫}_{0}^{π}$(sinx+cosx)dx
=sinx-cosx${|}_{0}^{π}$
=2,
∴T3=-20×26=-1280,
故答案为:-1280.
点评 本题考查二项式系数的性质,涉及定积分的计算,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
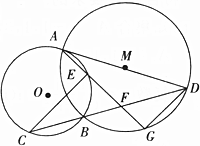 如图,已知⊙O和⊙M相交于A,B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧$\widehat{BD}$中点,连接AG分别交⊙O,BD于点E,F,连接CE.
如图,已知⊙O和⊙M相交于A,B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧$\widehat{BD}$中点,连接AG分别交⊙O,BD于点E,F,连接CE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com