
分析 显然m≠0,分当m>0与当m<0两种情况进行讨论,并进行变量分离即可得出答案.
解答 解:由f(mx)+mf(x)<0整理得:2mx<(m+$\frac{1}{m}$ )$\frac{1}{x}$,即2mx2<m+$\frac{1}{m}$ 恒成立.
①当m>0时,2x2<1+$\frac{1}{{m}^{2}}$,因为y=2x2在x∈[1,+∞)上无最大值,因此此时不合题意;
②当m<0时,2x2>1+$\frac{1}{{m}^{2}}$,因为y=2x2在x∈[1,+∞)上的最小值为2,所以1+$\frac{1}{{m}^{2}}$<2
即m2>1,解得m<-1或m>1(舍去).
综合可得:m<-1.
故答案为:m<-1.
点评 本题主要考查了恒成立问题的基本解法及分类讨论思想,属于中档题,解决恒成立问题通常可以利用分离变量转化为最值的方法求解.


科目:高中数学 来源: 题型:选择题
| A. | 3f(ln2)>2f(ln3) | B. | 3f(ln2)=2f(ln3) | ||
| C. | 3f(ln2)<2f(ln3) | D. | 3f(ln2)与2f(ln3)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
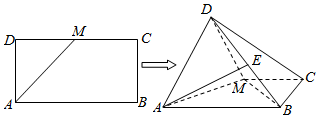
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
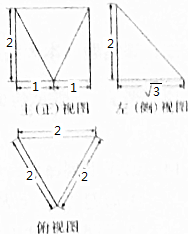
| A. | 8+$\sqrt{3}$ | B. | 10+$\sqrt{3}$ | C. | 8+$\sqrt{3}$+$\sqrt{7}$ | D. | 10+$\sqrt{3}$+$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com