
分析 根据指数幂的运算性质化简计算即可.
解答 解:(1)2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$=2×${3}^{\frac{1}{2}}×(\frac{3}{2})^{\frac{1}{3}}×1{2}^{\frac{1}{6}}$=2×27${\;}^{\frac{1}{6}}$×($\frac{9}{4}$)${\;}^{\frac{1}{6}}$×$1{2}^{\frac{1}{6}}$=2×(27×$\frac{9}{4}$×12)${\;}^{\frac{1}{6}}$=2×3=6,
(2)(2$\frac{7}{9}$)0.5+0.1-2+(2$\frac{10}{27}$)${\;}^{-\frac{2}{3}}$-3π°+$\frac{37}{48}$=$(\frac{25}{9})^{0.5}$+100+$(\frac{64}{27})^{-\frac{2}{3}}$-3+$\frac{37}{48}$=$\frac{5}{3}$+100+$\frac{9}{16}$-3+$\frac{37}{48}$=100,
(3)$\frac{(3{a}^{\frac{2}{3}}{b}^{\frac{1}{4}})×(-8{a}^{\frac{1}{2}}{b}^{\frac{1}{2}})}{-4\root{6}{{a}^{4}}•\sqrt{{b}^{3}}}$=-(3×8÷4)${a}^{\frac{2}{3}+\frac{1}{2}-\frac{2}{3}}$${b}^{\frac{1}{4}+\frac{1}{2}-\frac{3}{2}}$=-6${a}^{\frac{1}{2}}{b}^{-\frac{3}{4}}$
点评 本题考查了指数幂的运算运算性质,考查了学生的运算能了和转化能力,属于基础题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:高中数学 来源: 题型:解答题
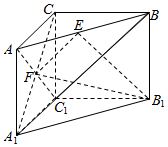 三棱柱ABC-A1B1C1中,侧棱AA1⊥面ABC,AC1⊥面CBA1,AC1∩A1C=F.
三棱柱ABC-A1B1C1中,侧棱AA1⊥面ABC,AC1⊥面CBA1,AC1∩A1C=F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com