
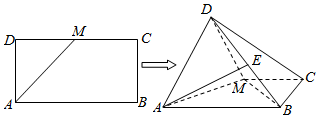
分析 (Ⅰ)推导出BM⊥AM,从而BM⊥平面ADM,由此能证明AD⊥BM.
(Ⅱ)法一:过点E作MB的平行线交DM于F,过点F作AM的垂线,垂足为H,连接HE,则∠EHF即为二面角E-AM-D的平面角,由此能求出当二面角E-AM-D大小为$\frac{π}{3}$时λ 的值.
法二:以M为原点,MA,MB 所在直线为x 轴,y 轴,建立空间直角坐标系,利用向量法能求出当二面角E-AM-D大小为$\frac{π}{3}$时λ 的值.
解答  证明:(Ⅰ)∵$AB=2,AM=BM=\sqrt{2}$,∴BM⊥AM,
证明:(Ⅰ)∵$AB=2,AM=BM=\sqrt{2}$,∴BM⊥AM,
又平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM,
∴BM⊥平面ADM.
又AD?平面ADM,∴AD⊥BM.
解:(Ⅱ)(方法一)过点E作MB的平行线交DM于F,
由BM⊥平面ADM,得EF⊥平面ADM,
在平面ADM中过点F作AM的垂线,垂足为H,连接HE,
则∠EHF即为二面角E-AM-D的平面角,大小为$\frac{π}{3}$.
设FM=x,则$DF=1-x,FH=\frac{{\sqrt{2}}}{2}x$,
在Rt△FHM 中,
由∠EFH=90°,∠EHF=60°,则$EF=\sqrt{3}FH=\frac{{\sqrt{6}}}{2}x$.
由EF∥MB,MB=2,
则$\frac{EF}{MB}=\frac{DF}{DM}$,即$\frac{\frac{\sqrt{6}x}{2}}{\sqrt{2}}=\frac{1-x}{1}$,解得x=4-2$\sqrt{3}$.
故当二面角E-AM-D 大小为$\frac{π}{3}$ 时,$\frac{DE}{DB}=2\sqrt{3}-3$,
即$λ=2\sqrt{3}-3$.
(方法二)以M为原点,MA,MB 所在直线为x 轴,y 轴,建立如图所示空间直角坐标系, M(0,0,0),$A(\sqrt{2},0,0)$,$B(0,\sqrt{2},0)$,$D(\frac{{\sqrt{2}}}{2},0,\frac{{\sqrt{2}}}{2})$,
M(0,0,0),$A(\sqrt{2},0,0)$,$B(0,\sqrt{2},0)$,$D(\frac{{\sqrt{2}}}{2},0,\frac{{\sqrt{2}}}{2})$,
且$\overrightarrow{DE}=λ\overrightarrow{DB}=λ(-\frac{{\sqrt{2}}}{2},\sqrt{2},-\frac{{\sqrt{2}}}{2})$,
所以,$E(\frac{{\sqrt{2}}}{2}(1-λ),\sqrt{2}λ,\frac{{\sqrt{2}}}{2}(1-λ))$,
设平面EAM 的法向量为$\overrightarrow m=(x,y,z)$,
则$\overrightarrow m•\overrightarrow{MA}=\sqrt{2}x=0$,
$\overrightarrow m•\overrightarrow{ME}=\frac{{\sqrt{2}}}{2}(1-λ)x+\sqrt{2}λy+\frac{{\sqrt{2}}}{2}(1-λ)z=0$,
所以,$\overrightarrow m=(0,λ-1,2λ)$.
又平面DAM 的法向量为$\overrightarrow n=(0,1,0)$,
所以,$|{cos<\overrightarrow m,\overrightarrow n>}|=\frac{{|{λ-1}|}}{{\sqrt{{{(λ-1)}^2}+4{λ^2}}}}=\frac{1}{2}$,
解得$λ=2\sqrt{3}-3$,或$λ=-2\sqrt{3}-3$ (舍去).
所以,$λ=2\sqrt{3}-3$.
点评 本题考查异面直线垂直的证明,考查满足二面角大小为$\frac{π}{3}$的实数值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
 如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=4,AA1=3,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.
如图,在棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为直角梯形,其中AB∥CD,AB⊥AD,AB=AC=2CD=4,AA1=3,过AC的平面分别与A1B1,B1C1交于E1,F1,且E1为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
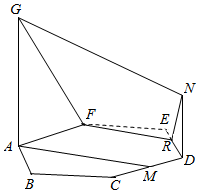 如图,已知ABCDEF是正六边形,GA、ND都垂直于平面ABCDEF,平面FGN交线段DE于点R,点M是CD的中点,AB=DN=1,AG=2.
如图,已知ABCDEF是正六边形,GA、ND都垂直于平面ABCDEF,平面FGN交线段DE于点R,点M是CD的中点,AB=DN=1,AG=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
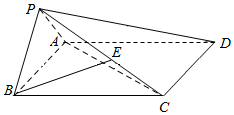 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD是边长为2的正方形,PA=PB,E为PC上的点,且BE⊥平面PAC.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD是边长为2的正方形,PA=PB,E为PC上的点,且BE⊥平面PAC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 结论正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com