
分析 (1)由题意可得-1,2是方程ax2+(a-2)x-2=0的两根(a>0),运用韦达定理,解方程可得a的值;
(2)由题意可得(a-2)x2+(a-2)x+1≥0恒成立,讨论a=2,a>2,判别式小于等于0,a<2不恒成立,解不等式即可得到所求a的范围;
(3)不等式可将其转化为(ax-2)(x+1)≥0,讨论a=0,a<0,a>0,$\frac{2}{a}$与-1的大小关系进行讨论,注意a=0的情况先讨论,从而进行求解.
解答 解:(1)由题意可得-1,2是方程ax2+(a-2)x-2=0的两根(a>0),
可得-1+2=$\frac{2-a}{a}$,-1×2=-$\frac{2}{a}$,
解得a=1;
(2)不等式ax2+(a-2)x-2≥2x2-3对x∈R恒成立,
即为(a-2)x2+(a-2)x+1≥0恒成立,
当a=2时,不等式即为1≥0恒成立;
当a>2时,△≤0即为(a-2)2-4(a-2)≤0,解得2<a≤6;
当a<2时,不等式不恒成立.
综上可得,a的取值范围是[2,6];
(3)不等式ax2+(a-2)x-2≥0.
即有(ax-2)(x+1)≥0.
①当a=0时,原不等式化为x+1≤0⇒x≤-1;
②当a<0时,原不等式化为(x+1)≤0,即x≤-1;
当$\frac{2}{a}$>-1,即a<-2时,原不等式等价于-1≤x≤$\frac{2}{a}$;
当$\frac{2}{a}$=-1,即a=-2时,原不等式等价于x=-1;
当$\frac{2}{a}$<-1,即-2<a<0时,原不等式等价于$\frac{2}{a}$≤x≤-1.
③当a>0时,$\frac{2}{a}$>-1,原不等式等价于x≥$\frac{2}{a}$或x≤-1.
综上所述:当a<-2时,原不等式的解集为;
当a=-2时,原不等式的解集为{-1};
当-2<a<0时,原不等式的解集为[$\frac{2}{a}$,-1];
当a=0时,原不等式的解集为(-∞,-1];
当a<-2时,原不等式的解集为[-1,$\frac{2}{a}$];
当a>0时,原不等式的解集为(-∞,-1]∪[$\frac{2}{a}$,+∞).
点评 本题考查二次不等式的解法和不等式恒成立恒成立问题的解法,以及含参二次不等式的解法,运用分类讨论的思想方法是解题的关键,考查运算能力,属于中档题和易错题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
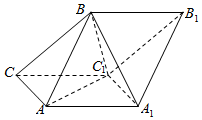 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为$\sqrt{3}$,且∠AA1C1为锐角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )
如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )| A. | $\sqrt{3}$π | B. | 2$\sqrt{3}$π | C. | 3$\sqrt{3}$π | D. | $\frac{3\sqrt{3}π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com