
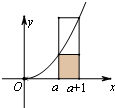
 ��ͼ��ʾ����ֱ��x=a��x=a+1��a��0����y=x2��x��Χ�ɵ��������ε����������ӦС���������ε����֮�䣬��a2��${��}_{a}^{a+1}$x2dx����a+1��2�����֮��?n��N*��$\frac{1}{n+1}$+$\frac{1}{n+2}$+��+$\frac{1}{2n}$��A��$\frac{1}{n}$+$\frac{1}{n+1}$+��+$\frac{1}{2n-1}$���������ʵ��A���ڣ�������
��ͼ��ʾ����ֱ��x=a��x=a+1��a��0����y=x2��x��Χ�ɵ��������ε����������ӦС���������ε����֮�䣬��a2��${��}_{a}^{a+1}$x2dx����a+1��2�����֮��?n��N*��$\frac{1}{n+1}$+$\frac{1}{n+2}$+��+$\frac{1}{2n}$��A��$\frac{1}{n}$+$\frac{1}{n+1}$+��+$\frac{1}{2n-1}$���������ʵ��A���ڣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{3}{5}$ | C�� | ln2 | D�� | ln$\frac{5}{2}$ |
���� ��A=A1+A2+A3+��+An�����ݶ����ֵĶ���õ���A1=-lnn+ln��n+1����ͬ�����A2��A3������An��ֵ�����������ɣ�
��� �⣺��A=A1+A2+A3+��+An��
������ã�$\frac{1}{n+1}$��A1��$\frac{1}{n}$��$\frac{1}{n+2}$��A2��$\frac{1}{n+1}$��$\frac{1}{n+3}$��A3��$\frac{1}{n+2}$������$\frac{1}{2n}$��An��$\frac{1}{2n-1}$��
��A1=${��}_{n}^{n+1}$$\frac{1}{x}$dx=lnx|${\;}_{n}^{n+1}$=ln��n+1��-lnn��
ͬ����A2=-ln��n+1��+ln��n+2����A3=-ln��n+2��+ln��n+3��������An=-ln��2n-1��+ln2n��
��A=A1+A2+A3+��+An
=-lnn+ln��n+1��-ln��n+1��+ln��n+2��-ln��n+2��+ln��n+3��-��-ln��2n-1��+ln2n
=ln2n-lnn
=ln2��
��ѡ��C��
���� ���⿼���˶����ֵļ�Ӧ�ã����ݶ����ֵĶ���õ�A1��A2��A3������An��ֵ�ǽ���Ĺؼ���������һ���е��⣮


 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{3}$ | B�� | 4$\sqrt{2}$ | C�� | 2$\sqrt{2}$ | D�� | 4$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
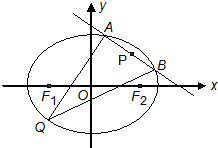 ��ͼ��ʾ����֪��ԲC�ķ���Ϊ$\frac{x^2}{2}+{y^2}$=1��F1��F2�ֱ�����ԲC�����ҽ��㣬ֱ��AB��y=kx+m��k��0������ԲC���ڲ�ͬ��A��B���㣮
��ͼ��ʾ����֪��ԲC�ķ���Ϊ$\frac{x^2}{2}+{y^2}$=1��F1��F2�ֱ�����ԲC�����ҽ��㣬ֱ��AB��y=kx+m��k��0������ԲC���ڲ�ͬ��A��B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1�� | B�� | [$\frac{1}{16}$��1�� | C�� | ��1��+�ޣ� | D�� | ��0��$\frac{1}{16}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��1] | B�� | [-3��-1] | C�� | ��-1��1] | D�� | [-3��-1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com