
分析 本题中两个向量的夹角为锐角,故应转化为两向量的内积为正,且不共线,由此条件转化的方程求参数的范围即可.
解答 解:$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(2,λ),向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角,
$\overrightarrow{a}$•$\overrightarrow{b}$>0且$\overrightarrow{a}$•$\overrightarrow{b}$≠|$\overrightarrow{a}$||$\overrightarrow{b}$|即3λ+2>0且λ≠6,
∴(-$\frac{2}{3}$,6)∪(6,+∞).
故答案为(-$\frac{2}{3}$,6)∪(6,+∞).
点评 本题考点是数量积表示两个向量的夹角,考查利用向量内积公式的变形形式求向量夹角的余弦,本题中两个向量的夹角为锐角,故可转化为两向量的内积大于0且两向量不共线,此转化有一个易漏点,即忘记考虑向量同向共线时向量内积也为正,做题时要注意转化的等价.本题属于基础公式应用题.


科目:高中数学 来源: 题型:选择题

| A. | 2.7岁 | B. | 3.1岁 | C. | 3.2岁 | D. | 4岁 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
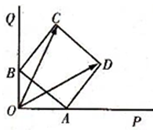 如图,边长为2的正方形ABCD的顶点A,B分别在两条互相垂直的射线OP,OQ上滑动,则$\overrightarrow{OC}$•$\overrightarrow{CD}$的最大值为8.
如图,边长为2的正方形ABCD的顶点A,B分别在两条互相垂直的射线OP,OQ上滑动,则$\overrightarrow{OC}$•$\overrightarrow{CD}$的最大值为8.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{89}{2}$ | B. | 61 | C. | 39 | D. | 72 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{5}{2}$) | B. | ($\frac{5}{2}$,+∞) | C. | (-1,$\frac{5}{2}$) | D. | ($\frac{5}{2}$,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com