
����Ŀ����֪�Ȳ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ���ȱ�����
���ȱ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��
��![]() ��
��![]() .
.
��1����![]() ����
����![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ����
����![]() .
.
���𰸡���1��![]() ����2��21��
����2��21��![]() .
.
�������������������1����Ȳ�����![]() ����Ϊ
����Ϊ![]() ���ȱ�����
���ȱ�����![]() ����Ϊ
����Ϊ![]() ������֪�������
������֪�������![]() ����д��ͨ�ʽ����2����
����д��ͨ�ʽ����2����![]() �����
�����![]() ��ֵ�������
��ֵ�������![]() ��ֵ�����
��ֵ�����![]() ��
��
�����������Ȳ�����![]() ����Ϊ
����Ϊ![]() ���ȱ�����
���ȱ�����![]() ����Ϊ
����Ϊ![]() ��
��![]() ����
����![]() .
.
��1����![]() �����
�����![]() ��
��![]() ��
��
��![]() .
.
��2����![]() �����
�����![]() ��3��
��3��
��![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() ��
��
��![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() .
.
�����͡������
��������
20
����Ŀ����ͼ����ֱ֪����������![]() �ཻ��
�ཻ��![]() ��������
��������![]() ��
�� ![]() ��
��![]() ��
��![]() ���ҵ�
���ҵ�![]() ������Ϊ
������Ϊ![]() .
.
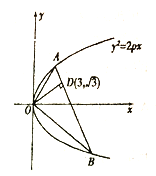
��1����![]() ��ֵ��
��ֵ��
��2����![]() Ϊ�����ߵĽ�����
Ϊ�����ߵĽ����� ![]() Ϊ����������һ������
Ϊ����������һ������![]() ����Сֵ.
����Сֵ.
���𰸡���1��![]() .��2��4.
.��2��4.
�������������������1����A��x1��y1����B��x2��y2������AB��OD��kOD=![]() ���ɵ�ֱ��AB��б��k=-
���ɵ�ֱ��AB��б��k=-![]() ���õ�ֱ��AB�ķ���Ϊ
���õ�ֱ��AB�ķ���Ϊ![]() ���������߷���������Ϊ
���������߷���������Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() �����ɽ��
�����ɽ��![]() ��ֵ��
��ֵ��
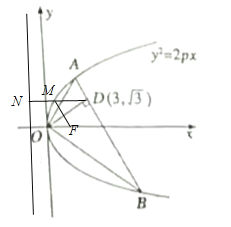
��2������M��ֱ�ߵĴ���MN������ΪN����|MF|=|MN|���������߶���֪![]() ����СֵΪ
����СֵΪ![]() �㵽������
�㵽������![]() �ߵľ���.
�ߵľ���.
���������
��1����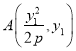 ��
�� 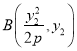 ��
�� ![]() ��
��
��![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��![]() .��
.��![]() ������ʽ��
������ʽ��
������![]() ����
����![]() ����
����![]() ��
��![]() ����
����
![]() ����
����![]() ����
����![]() ����
����![]() .
.
��2������M��ֱ�ߵĴ���MN������ΪN����|MF|=|MN|���������߶���֪![]() ����СֵΪ
����СֵΪ![]() �㵽������
�㵽������![]() �ߵľ��������߷���Ϊ
�ߵľ��������߷���Ϊ![]() �����
�����![]() ����СֵΪDN=4.
����СֵΪDN=4.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f�䣨x�����溯��f��x����x��R���ĵ�������f����1��=0����x��0ʱ��xf�䣨x����f��x����0����ʹ��f��x����0������x��ȡֵ��Χ�ǣ� ��
A.�����ޣ���1���ȣ�0��1��
B.����1��0���ȣ�1��+�ޣ�
C.�����ޣ���1���ȣ���1��0��
D.��0��1���ȣ�1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������̨![]() ����
���� ![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е�.
���е�.
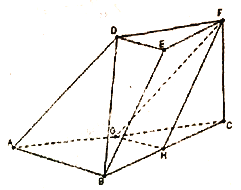
��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɽǣ���ǣ��Ĵ�С.
���ɽǣ���ǣ��Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ����� ![]() ��,����
��,���� ![]() ,
, ![]() ����
���� ![]() �ɵȱ�����.
�ɵȱ�����.
��1�������� ![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2���� ![]() ����
Ϊ���� ![]() ��ǰ
��ǰ ![]() ��ͣ��Ҵ���
��ͣ��Ҵ��� ![]() ��ʹ��
��ʹ�� ![]() ��������ʵ��
��������ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ž�Ӫijһ����Ʒר���꣬��֪������Ʒ�Ľ���Ϊÿ��40Ԫ���õ�ÿ�����������ټ��������۵���x��Ԫ/����֮��Ĺ�ϵ����ͼ��һ���߱�ʾ��ְ��ÿ��ÿ�¹���Ϊ1000Ԫ���õ껹Ӧ��������������Ϊÿ��10000Ԫ.

��1����y��ʾΪx�ĺ�����
��2�������ۼ�Ϊÿ��50Ԫʱ���õ�������֧ƽ�⣨������Ϊ�㣩����õ��ְ��������
��3�����õ�ֻ��20��ְ���������۵��۶�Ϊ����Ԫʱ����ר����ɻ�����������ע������=����-֧����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ ![]() ���ϡ��¶���ֱ���
���ϡ��¶���ֱ��� ![]() ����
���� ![]() ��
�� ![]() ���е㣬��
���е㣬�� ![]() ����
���� ![]() .
.
��1������Բ ![]() �ı����̣�
�ı����̣�
��2���� ![]() ��ֱ��
��ֱ�� ![]() ����Բ
����Բ ![]() ���ڲ�ͬ������
���ڲ�ͬ������ ![]() ����
���� ![]() ����������ֵ.
����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x+ ![]() +lnx��a��R�� ������f��x����x=1��ȡ�ü�ֵ����a��ֵ��
+lnx��a��R�� ������f��x����x=1��ȡ�ü�ֵ����a��ֵ��
������f��x�������䣨1��2���ϵ�����������a��ȡֵ��Χ��
�������ۺ���g��x��=f'��x����x����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ABEF��ƽ��ABC���ı���ABEFΪ���Σ�AC=BC��OΪAB���е㣬OF��EC�� ������֤��OE��FC��
������ ![]() =
= ![]() ʱ��������F��CE��B������ֵ��
ʱ��������F��CE��B������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com