
| A. | (1,+∞) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (1,2) |
分析 利用点与圆的关系求解.
解答 解:当点(1,1)在圆(x-a)2+(y+a)2=4的内部,点(0,2)在圆(x-a)2+(y+a)2=4的圆的外面时,
$\left\{\begin{array}{l}{(1-a)^{2}+(1+a)^{2}<4}\\{(0-a)^{2}+(2+a)^{2}>4}\end{array}\right.$,解得0<a<1;
当点(0,2)在圆(x-a)2+(y+a)2=4的内部,点(1,1)在圆(x-a)2+(y+a)2=4的圆的外面时,
$\left\{\begin{array}{l}{(1-a)^{2}+(1+a)^{2}>4}\\{(0-a)^{2}+(2+a)^{2}<4}\end{array}\right.$.解得-2<a<-1,不满足正实数a.
综上,正实数a的取值范围是(0,1).
故选:C.
点评 本题考查正实数的取值范围的求法,是基础题,解题时要认真审题,注意点与圆的位置关系的性质的合理运用.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{17}{40}$ | B. | -$\frac{5}{16}$ | C. | -$\frac{34}{45}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
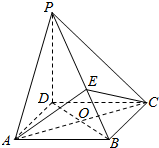 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
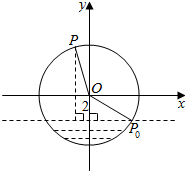 如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.
如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
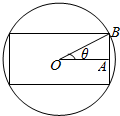 把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )
把截面半径为5的圆形木头锯成面积为y的矩形木料,如图,点O为圆心,OA⊥OB,设∠AOB=θ,把面积y表示为θ的表达式,则有( )| A. | y=50cos2θ | B. | y=25sinθ | C. | y=25sin2θ | D. | y=50sin2θ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com