
分析 由题意画出图形,延长BO交平面ACD于点M,则$\overrightarrow{OM}$=λ1$\overrightarrow{OA}$+λ2$\overrightarrow{OC}$+λ3$\overrightarrow{OD}$,且λ1+λ2+λ3=1.把已知向量等式变形,得到$\overrightarrow{BO}$=$\frac{1+sinα+cosα}{\sqrt{2}-1}\overrightarrow{OM}$,然后利用三角函数求得VO-ACD的最小值,同理求出VO-BCD的最小值,则VO-ABD+VO-ABC的最大值可求.
解答 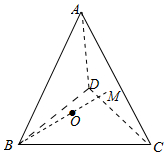 解:如图,延长BO交平面ACD于点M,则$\overrightarrow{OM}$=λ1$\overrightarrow{OA}$+λ2$\overrightarrow{OC}$+λ3$\overrightarrow{OD}$,且λ1+λ2+λ3=1.
解:如图,延长BO交平面ACD于点M,则$\overrightarrow{OM}$=λ1$\overrightarrow{OA}$+λ2$\overrightarrow{OC}$+λ3$\overrightarrow{OD}$,且λ1+λ2+λ3=1.
根据题意,$\overrightarrow{OA}$+($\sqrt{2}$-1)$\overrightarrow{OB}$+sinα$\overrightarrow{OC}$+cosα$\overrightarrow{OD}$=$\overrightarrow{0}$,
则$\overrightarrow{BO}=\frac{1}{\sqrt{2}-1}$($\overrightarrow{OA}+sinα\overrightarrow{OC}+cosα\overrightarrow{OD}$)
=$\frac{1+sinα+cosα}{\sqrt{2}-1}(\frac{1}{1+sinα+cosα}\overrightarrow{OA}+\frac{sinα}{1+sinα+cosα}\overrightarrow{OC}+\frac{cosα}{1+sinα+cosα}\overrightarrow{OD})$
=$\frac{1+sinα+cosα}{\sqrt{2}-1}\overrightarrow{OM}$,
由于$\frac{1+sinα+cosα}{\sqrt{2}-1}=\frac{\sqrt{2}sin(α+\frac{π}{4})+1}{\sqrt{2}-1}≤\frac{\sqrt{2}+1}{\sqrt{2}-1}$,
∴$|\overrightarrow{BO}|≤\frac{\sqrt{2}+1}{\sqrt{2}-1}|\overrightarrow{OM}|$,
当$\overrightarrow{BO}=\frac{\sqrt{2}+1}{\sqrt{2}-1}\overrightarrow{OM}$时,$\frac{OB}{BM}$最大,$\frac{OM}{BM}$最小,因此VO-ACD最小,
此时α=$\frac{π}{4}$,
此时,$\frac{OB}{BM}=\frac{\sqrt{2}+1}{2\sqrt{2}},\frac{OM}{BM}=\frac{\sqrt{2}-1}{2\sqrt{2}}$=$\frac{2-\sqrt{2}}{4}$,
故VO-ACD的最小为$\frac{2-\sqrt{2}}{4}V$;
同理,延长AO交平面BCD于点N,则$\overrightarrow{ON}={λ}_{1}\overrightarrow{OB}+{λ}_{2}\overrightarrow{OC}+{λ}_{3}\overrightarrow{OD}$,且λ1+λ2+λ3=1,
由$\overrightarrow{OA}$+($\sqrt{2}$-1)$\overrightarrow{OB}$+sinα$\overrightarrow{OC}$+cosα$\overrightarrow{OD}$=$\overrightarrow{0}$,得
$\overrightarrow{AO}$=($\sqrt{2}$-1)$\overrightarrow{OB}$+sinα$\overrightarrow{OC}$+cosα$\overrightarrow{OD}$
=($\sqrt{2}-1+sinα+cosα$)[$\frac{\sqrt{2}-1}{\sqrt{2}-1+sinα+cosα}\overrightarrow{OB}+\frac{sinα}{\sqrt{2}-1+sinα+cosα}\overrightarrow{OC}+\frac{cosα}{\sqrt{2}-1+sinα+cosα}\overrightarrow{OD}$]
=$(\sqrt{2}-1+sinα+cosα)\overrightarrow{ON}$,
由于$\sqrt{2}-1+sinα+cosα=\sqrt{2}sin(α+\frac{π}{4})+\sqrt{2}-1$$≤2\sqrt{2}-1$,
∴$|\overrightarrow{AO}|≤(2\sqrt{2}-1)|\overrightarrow{ON}|$,
当$\overrightarrow{AO}=(2\sqrt{2}-1)\overrightarrow{ON}$时,$\frac{OA}{AN}$最大,$\frac{ON}{AN}$最小,因此VO-BCD最小,
此时$α=\frac{π}{4}$,
此时,$\frac{OA}{AN}=\frac{2\sqrt{2}-1}{2\sqrt{2}}$,$\frac{ON}{AN}=\frac{1}{2\sqrt{2}}$=$\frac{\sqrt{2}}{4}$,
故VO-BCD的最小值为$\frac{\sqrt{2}}{4}V$;
∴VO-ABD+VO-ABC的最大值为$V-\frac{2-\sqrt{2}}{4}V-\frac{\sqrt{2}}{4}V=\frac{1}{2}V$.
故答案为:$\frac{2-\sqrt{2}}{4}V$;$\frac{1}{2}V$;$\frac{\sqrt{2}}{4}V$.
点评 本题考查棱柱、棱锥及棱台体积的求法,考查数学转化思想方法,训练了共面向量基本定理的应用,训练了利用三角函数求最值,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{x}$=$\overrightarrow{a}$ | B. | $\overrightarrow{x}$与$\overrightarrow{a}$反向 | C. | |$\overrightarrow{x}$|=|$\overrightarrow{a}$|且$\overrightarrow{x}$与$\overrightarrow{a}$反向 | D. | $\overrightarrow{x}$与$\overrightarrow{a}$是相反向量 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
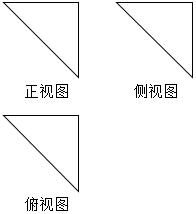
| A. | 8 | B. | 4$\sqrt{3}$+4 | C. | 4$\sqrt{2}$+4 | D. | 6+2$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com