
 x
x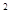 -ax+(a-1)
-ax+(a-1) ,
, 。
。 的单调性;(2)若
的单调性;(2)若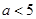 ,设
,设 ,
, ,x
,x

 ,x
,x
 x
x ,有
,有 .
.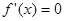 时的驻点,再由
时的驻点,再由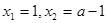 的大小关系讨论导函数的正负,从而确定函数的单调性;(2)(ⅰ)由
的大小关系讨论导函数的正负,从而确定函数的单调性;(2)(ⅰ)由 得出
得出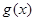
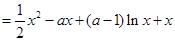 ;求出
;求出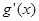 ,由
,由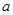 的范围得从而得出出
的范围得从而得出出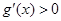 ,函数单调递增;(ⅱ)由
,函数单调递增;(ⅱ)由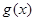 单调递增定义可推导.
单调递增定义可推导. x2-ax+(a-1)lnx,其中a>1,
x2-ax+(a-1)lnx,其中a>1,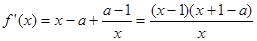
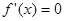 解得:
解得: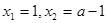 .
.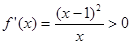

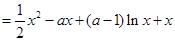
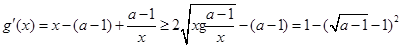 .10分
.10分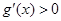 ,即g(x)在(0, +∞) 上单调递增. .11分
,即g(x)在(0, +∞) 上单调递增. .11分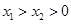 时有
时有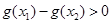 ,即
,即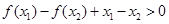 ,
, ,当
,当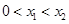 时,有
时,有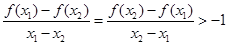 14分
14分

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源:不详 题型:单选题
 及其导数
及其导数 ,若存在
,若存在 ,使得
,使得 =
= ,则称
,则称 是
是 的一个“巧值点”,下列函数中,有“巧值点”的函数的个数是( )
的一个“巧值点”,下列函数中,有“巧值点”的函数的个数是( ) ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤
| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com