
某花店每天以每枝 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:枝,
(单位:枝, )的函数解析式;
)的函数解析式;
(2)花店记录了 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
①假设花店在这 天内每天购进
天内每天购进 枝玫瑰花,求这
枝玫瑰花,求这 天的日利润(单位:元)的平均数;
天的日利润(单位:元)的平均数;
②若花店一天购进 枝玫瑰花,以
枝玫瑰花,以 天记录的的各需求量的频率作为各需求量发生的概率,
天记录的的各需求量的频率作为各需求量发生的概率,
【文科学生继续做】 求当天的利润不少于 元的概率.
元的概率.
【理科学生继续做】 求当天的利润 (单位:元)的分布列与数学期望.
(单位:元)的分布列与数学期望.
(1)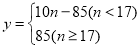 ,
, ;
;
(2)【文科学生继续做】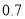 ,
,
【理科生继续做】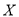 (单位:元)的分布列为
(单位:元)的分布列为
|
|
|
|
|
|
|
|
|
|
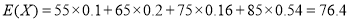 .
.
【解析】
试题分析:(1)根据题意可知,利润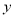 应是当天需求量
应是当天需求量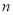 的分段函数,需对
的分段函数,需对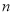 与购进量
与购进量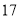 的大小关系进行分类讨论:当
的大小关系进行分类讨论:当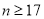 时,购进的玫瑰花全部都能卖出,∴利润
时,购进的玫瑰花全部都能卖出,∴利润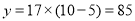 ,当
,当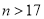 时,购进的玫瑰花卖出
时,购进的玫瑰花卖出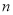 枝,余下的
枝,余下的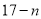 枝当做垃圾处理,∴利润
枝当做垃圾处理,∴利润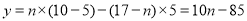 ;(2)【文科生继续做】由(1)可知,要满足当天利润不少于
;(2)【文科生继续做】由(1)可知,要满足当天利润不少于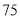 元,只需当天需求量
元,只需当天需求量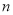 满足不等式
满足不等式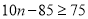 即可,解得
即可,解得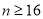 ,再由条件中给出的频数分布表,结合条件利用频率来代替概率,可得所求概率为
,再由条件中给出的频数分布表,结合条件利用频率来代替概率,可得所求概率为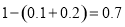
【理科生继续做】通过(1)中得到的函数表达式可知,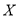 的取值有四种情况:
的取值有四种情况: ,再由条件中给出的频数分布表,结合条件利用频率来代替概率,可得:
,再由条件中给出的频数分布表,结合条件利用频率来代替概率,可得: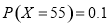 ,
,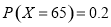 ,
,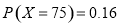 ,
,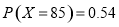 .从而可得
.从而可得
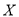 (单位:元)的分布列为
(单位:元)的分布列为
|
|
|
|
|
|
|
|
|
|
.期望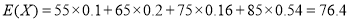 .
.
试题解析:(1)当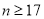 时,购进的玫瑰花全部都能卖出,∴利润
时,购进的玫瑰花全部都能卖出,∴利润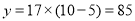 ,当
,当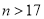 时,购进的玫瑰花卖出
时,购进的玫瑰花卖出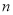 枝,余下的
枝,余下的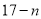 枝当做垃圾处理,∴利润
枝当做垃圾处理,∴利润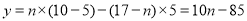 ,
,
综上可知,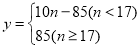 ,
, 5分;
5分;
(2)【文科生继续做】由(1)可知,要使当天利润不少于 元,日需求量
元,日需求量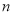 需满足
需满足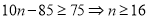 ,故所求概率为
,故所求概率为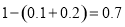 ,
,
【理科生继续做】由(1)可知,随机变量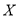 的取值有四种情况:
的取值有四种情况: ,
,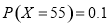 ,
,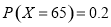 ,
,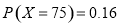 ,
,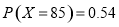 .
.
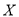 (单位:元)的分布列为
(单位:元)的分布列为
|
|
|
|
|
|
|
|
|
|
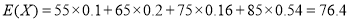 . 13分(每个结果各1分)
. 13分(每个结果各1分)
考点:1.函数解析式的常见求法;2.概率的运用.


科目:高中数学 来源:2014-2015学年浙江省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分8分)
已知函数
(1) 若函数 的图象经过点
的图象经过点 ,求
,求 的值;
的值;
(2) 判断并证明函数 的奇偶性;
的奇偶性;
(3) 比较 与
与 的大小,并写出必要的理由.
的大小,并写出必要的理由.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省湖州市高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分15分)设函数 ,
,
(1)求证:不论 为何实数
为何实数 总为增函数;
总为增函数;
(2)确定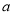 的值,使
的值,使 为奇函数及此时
为奇函数及此时 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:选择题
如图是正方体的平面展开图,则在这个正方体中的AB与CD的
位置关系是( )
A.AB∥CD B.AB⊥CD C.异面且成90?角 D.异面且成60?角
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高二上学期第一次阶段测试数学试卷(解析版) 题型:填空题
已知如图是一个空间几何体的三视图,则该几何体的外接球的表面积为 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南郑州外国语学校高二上学期第一次月考理科数学卷(解析版) 题型:解答题
(本题满分12分)在 中,角
中,角 所对的边分别为
所对的边分别为 且满足
且满足
(1)求角 的大小;
的大小;
(2)求 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com