
设函数 ,
, 且
且 .曲线
.曲线 在点
在点
处的切线的斜率为 .
.
(1)求 的值;
的值;
(2)若存在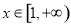 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
(1)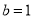 ;(2)
;(2)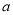 的取值范围是
的取值范围是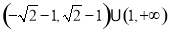 .
.
【解析】
试题分析:(1)根据条件曲线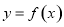 在点
在点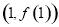 处的切线的斜率为
处的切线的斜率为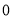 ,可以将其转化为关于
,可以将其转化为关于 ,
,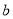 的方程,进而求得
的方程,进而求得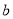 的值:
的值: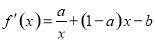 ,
,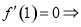
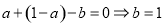 ;(2)根据题意分析可得若存在
;(2)根据题意分析可得若存在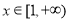 ,使得不等式
,使得不等式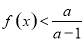 成立,只需
成立,只需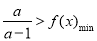 即可,因此可通过探求
即可,因此可通过探求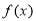 的单调性进而求得
的单调性进而求得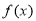 的最小值,进而得到关于
的最小值,进而得到关于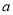 的不等式即可,而由(1)可知
的不等式即可,而由(1)可知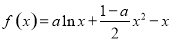 ,则
,则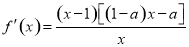 ,因此需对
,因此需对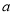 的取值范围进行分类讨论并判断
的取值范围进行分类讨论并判断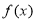 的单调性,从而可以解得
的单调性,从而可以解得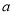 的取值范围是
的取值范围是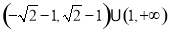 .
.
试题解析:(1)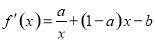 ,2分
,2分
由曲线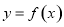 在点
在点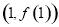 处的切线的斜率为
处的切线的斜率为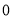 ,得
,得 ,3分
,3分
即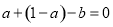 ,
,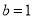 ; 4分(2)由(1)可得,
; 4分(2)由(1)可得,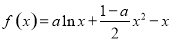 ,
,
 , 5分
, 5分
令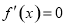 ,得
,得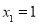 ,
,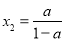 ,而
,而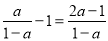 , 6分
, 6分
①当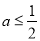 时,
时,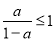 ,
,
在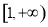 上,
上,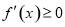 ,
, 为增函数,
为增函数,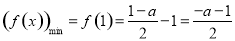 ,
,
令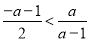 ,即
,即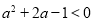 ,解得
,解得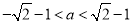 . 8分
. 8分
②当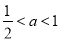 时,
时,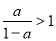 ,
,
|
|
|
|
|
|
|
|
|
| 极小值 |
|
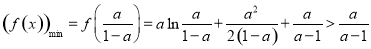 ,
,
不合题意,无解,10分
③当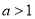 时,显然有
时,显然有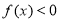 ,
, ,∴不等式
,∴不等式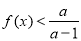 恒成立,符合题意, 12分
恒成立,符合题意, 12分
综上,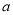 的取值范围是
的取值范围是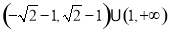 . 13分
. 13分
考点:导数的运用.


科目:高中数学 来源:2014-2015学年浙江省湖州市高一上学期期中考试数学试卷(解析版) 题型:选择题
已知 在
在 上是
上是 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C.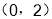 D.(1,2]
D.(1,2]
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,在三棱锥P ? ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.

(1)证明平面PBF⊥平面PAC;
(2)判断AE是否平行平面PFD?并说明理由;
(3)若PC = AB = 2,求三棱锥P ? DEF的体积.
查看答案和解析>>
科目:高中数学 来源:2015届北京市高三8月开学测试数学试卷(解析版) 题型:解答题
某花店每天以每枝 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:枝,
(单位:枝, )的函数解析式;
)的函数解析式;
(2)花店记录了 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
①假设花店在这 天内每天购进
天内每天购进 枝玫瑰花,求这
枝玫瑰花,求这 天的日利润(单位:元)的平均数;
天的日利润(单位:元)的平均数;
②若花店一天购进 枝玫瑰花,以
枝玫瑰花,以 天记录的的各需求量的频率作为各需求量发生的概率,
天记录的的各需求量的频率作为各需求量发生的概率,
【文科学生继续做】 求当天的利润不少于 元的概率.
元的概率.
【理科学生继续做】 求当天的利润 (单位:元)的分布列与数学期望.
(单位:元)的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com