
(本小题满分12分)如图,在三棱锥P ? ABC中,PC⊥平面ABC,△ABC为正三角形,D,E,F分别是BC,PB,CA的中点.

(1)证明平面PBF⊥平面PAC;
(2)判断AE是否平行平面PFD?并说明理由;
(3)若PC = AB = 2,求三棱锥P ? DEF的体积.
(1)证明:平面PBF⊥平面PAC;(2)AE不平行平面PFD;(3) .
.
【解析】
试题分析:(Ⅰ)要证明平面PBF⊥平面PAC,知需要在平面PBF内找到一条直线与平面PAC垂直即可,由题意可以选择证明BF⊥平面PAC;(2)用反证法证明,假设AE平行平面PFD,然后通过题目的条件推出矛盾即可;(3)因为E是PB的中点,所以三棱锥 三棱锥
三棱锥 是同底等高的,所以
是同底等高的,所以 ,因此
,因此 .
.
解:(1)∵PC⊥平面ABC,BF 平面ABC,∴PC⊥BF.
平面ABC,∴PC⊥BF.
∵△ABC为正三角形,F 是CA的中点 ∴BF⊥AC.又∵PC∩AC ? C.
∴BF⊥平面PAC. ∵BF 平面PBF,∴平面PBF⊥平面PAC. 4分
平面PBF,∴平面PBF⊥平面PAC. 4分
(2)AE不平行平面PFD.
反证法:假设AE∥平面PFD.∵AB∥FD,FD 平面PFD,AB
平面PFD,AB 平面PFD
平面PFD
∴AB∥平面PFD.∵AE、AB 是平面ABE内两条相交直线,
∴平面ABE∥平面PFD.
而∵P∈平面ABE,P∈平面PFD,矛盾. 则假设不成立.即AE不平行平面PFD. 8分
(3)∵E是PB的中点 ∴  .
.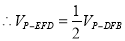
因为D,F是BC,AC的中点,所以
又因为 PC⊥平面ABC
所以 =
= ×
× ×
× S△ABC ×PC=
S△ABC ×PC= ×
× ×
×
 ×
× ?
? . 12分
. 12分
考点: 1、面面垂直的判定定理;2、反证法;3、三棱锥体积公式.


科目:高中数学 来源:2014-2015学年湖北武汉二中、龙泉中学高一上学期期中考试数学试卷(解析版) 题型:选择题
函数 在区间
在区间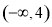 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省实验班高二10月月考理科数学试卷(解析版) 题型:选择题
在长方体 中,
中, .若
.若 分别为线段
分别为线段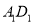 ,
, 的中点,则直线
的中点,则直线 与平面
与平面 所成角的正弦值为( )
所成角的正弦值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:填空题
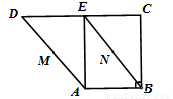
如图,在直角梯形ABCD中, ,M、N分别是AD、BE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
,M、N分别是AD、BE的中点,将三角形ADE沿AE折起,下列说法正确的是 (填上所有正确的序号)。
①不论D折至何位置(不在平面ABC内)都有 ;
;
②不论D折至何位置都有 ;
;
③不论D折至何位置(不在平面ABC内)都有 ;
;
④在折起过程中,一定存在某个位置,使 。
。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省杭州市高二10月月考数学试卷(解析版) 题型:选择题
在下列命题中,不是公理的是( )
A.平行于同一个平面的两个平面相互平行
B.过不在同一条直线上的三点,有且只有一个平面
C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内
D.如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com