
| A. | (x+4)(x2-2x+2)>3 | B. | x+4>3(x2-2x+2) | C. | $\frac{1}{{{x^2}-2x+2}}>\frac{3}{x+4}$ | D. | $\frac{{{x^2}-2x+2}}{x+4}<\frac{1}{3}$ |
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
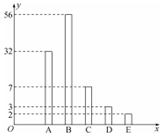 某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为A、B、C、D、E五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 120° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=8,AD=4,AB=2DC=4$\sqrt{5}$.
如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=8,AD=4,AB=2DC=4$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [3,+∞) | C. | (-∞,1] | D. | (-∞,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com