练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
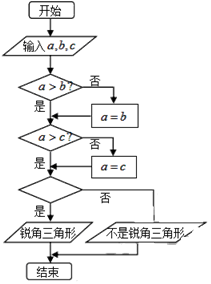
    4．如图程序框图中，若输入互不相等的三个正实数a，b，c，要求判断△ABC的形状，则空白的判断框中应填入（　　）
    A．a2+b2＞c2？B．a2+c2＞b2？C．b2+c2＞a2？D．b2+a2=c2？

    分析 根据流程图的功能知是比较a、b、c中的最大数用变量a表示并判断和输出是否为锐角三角形，
    分析三个判断框即可得出结论．

    解答 解：由流程图可知比较a、b、c中的最大数用变量a表示并判断和输出是否为锐角三角形，
    第一个判断框是判断a与b的大小，并把较大值赋值变量a；
    第二个判断框是判断最a与c的大小，并将最大数赋值变量a；
    第三个判断框是判断是否为锐角三角形，应填入：b2+c2＞a2？；
    故选：C．

    点评 本题考查了算法与程序框图的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．正四面体侧面与底面所成二面角的余值$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知f（x）=ax2+bx，其中-1≤a＜0，b＞0，则“存在x∈[0，1]，|f（x）|＞1”是“a+b＞1”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

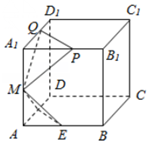    12．已知棱长为l的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1，A1D1上，且A1P=A1Q=x，0＜x＜1，设面MEF∩面MPQ=l，则下列结论中不成立的是（　　）
    A．l∥面ABCDB．l⊥AC
    C．面MEF与面MPQ垂直D．当x变化时，l是定直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知三棱锥A-BCD四个顶点都在半径为3的球面上，且BC过球心，当三棱锥A-BCD的体积最大时，则三棱锥A-BCD的表面积为（　　）
    A．$18+6\sqrt{3}$B．$18+8\sqrt{3}$C．$18+9\sqrt{3}$D．$18+10\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若复数z满足（1+i）z=|$\sqrt{3}$+i|，则在复平面内，z对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．等腰三角形ABC绕底边上的中线AD所在的直线旋转所得的几何体是（　　）
    A．圆台B．圆锥C．圆柱D．球

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．在海岸A处，发现北偏东45°方向，距离A为$（\sqrt{3}-1）$海里的B处有一艘走私船，在A处北偏西75°方向，距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船，此时，走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
    （Ⅰ）问C船与B船相距多少海里？C船在B船的什么方向？
    （Ⅱ）问缉私艇沿什么方向行驶才能最快追上走私船？并求出所需时间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．某区实验幼儿园对儿童记忆能力x与识图能力y进行统计分析，得到如下数据：
    记忆能力x46810
    识图能力y3568
    由表中数据，求得线性回归方程为$y=\frac{4}{5}x+a$，当江小豆同学的记忆能力为12时，预测他的识图能力为（　　）
    A．9B．9.5C．10D．11.5

    查看答案和解析>>

    同步练习册答案