
| A. | $18+6\sqrt{3}$ | B. | $18+8\sqrt{3}$ | C. | $18+9\sqrt{3}$ | D. | $18+10\sqrt{3}$ |
分析 判断几何体的体积最大时的位置,然后求解三棱锥的表面积.
解答 解:三棱锥A-BCD四个顶点都在半径为3的球面上,且BC过球心,三棱锥A-BCD的体积最大,
可知BC是球的直径,D在大圆上,当三角形DBC是等腰直角三角形时,面积最大,如果A与球心的连线与BCD平面垂直,则几何体的体积最大;如图:
则三棱锥A-BCD的表面积: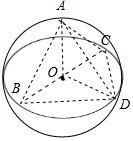
此时OA=OB=OD=OC=3,AB=AD=AC=3$\sqrt{2}$,
BD=DC=3$\sqrt{2}$,三棱锥的表面积为:2×$\frac{1}{2}×6×3$+2×$\frac{\sqrt{3}}{4}×(3\sqrt{2})^{2}$=18+9$\sqrt{3}$.
故选:C.
点评 本题考查几何体的外接球,几何体的体积与几何体的位置关系的判断,表面积的求法,考查空间想象能力以及计算能力.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{8}$ | B. | $\frac{11π}{16}$ | C. | $\frac{9π}{16}$ | D. | $\frac{7π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
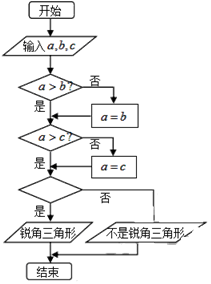 如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )
如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com