
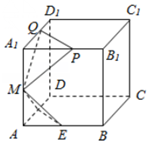
 已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )| A. | l∥面ABCD | B. | l⊥AC | ||
| C. | 面MEF与面MPQ垂直 | D. | 当x变化时,l是定直线 |
分析 由已知条件推导出l∥EF,从而得到l∥面ABCD;由MN是运动的,得到面MEF与面MPQ所成二面角是不确定的,从而平面MEF与平面MPQ不垂直;EF∥BD,l∥EF,EF与AC所成的角为90°,从而l与AC垂直;M是一个确定的点,从而当x变化时,l是定直线.
解答 解:对于A,∵棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,
又P、Q分别在线段A1B1、A1D1上,且A1P=A1Q=x,0<x<1,
∵QP∥EF,EF∥中截面,由平面与平面平行的性质定理,可知:面MEF∩面MPQ=l,由平面与平面平行的性质定理可知:l∥面ABCD,故A结论正确;
对于B,∵正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点∴AC⊥EF,由三垂线定理可知:l⊥AC,故B结论正确.
对于C,∵MN是运动的,∴面MEF与面MPQ所成二面角是不确定的,∴平面MEF与平面MPQ不垂直,故C不正确;
对于D,∵M是AA1的中点,是一个确定的点,∴当x变化时,l是过M与EF平行的定直线,故D正确.
故选:C.
点评 本题考查空间想象能力,直线与平面,直线与直线的位置关系,考查逻辑推理能力.属于中档题,


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 108 | C. | 114 | D. | 124 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{8}$ | B. | $\frac{11π}{16}$ | C. | $\frac{9π}{16}$ | D. | $\frac{7π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
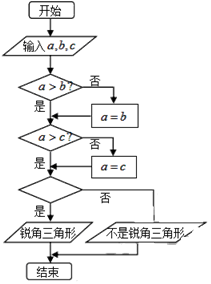 如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )
如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com