
分析 (1)由已知利用同角三角函数基本关系式即可计算得解.
(2)由已知利用同角三角函数基本关系式,结合cosα<0,可求cosα的值.
解答 解:(1)因为tanα=2,
所以$\frac{3sinα-2cosα}{sinα-cosα}=\frac{3tanα-2}{tanα-1}=\frac{3×2-2}{2-1}=4$
(2)解法1:由$\frac{sinα}{cosα}$=tanα=2,得sinα=2cosα,又sin2α+cos2α=1,
故5cos2α=1,即cos2α=$\frac{1}{5}$,因为α是第三象限角,cosα<0,所以cosα=-$\frac{\sqrt{5}}{5}$.
解法2:因为cos2α=$\frac{co{s}^{2}α}{co{s}^{2}α+si{n}^{2}α}$=$\frac{1}{1+ta{n}^{2}α}$=$\frac{1}{1+{2}^{2}}$=$\frac{1}{5}$,
又因为α是第三象限角,所以cosα<0,
所以cosα=-$\frac{\sqrt{5}}{5}$.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
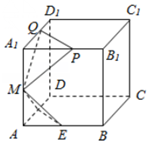 已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )| A. | l∥面ABCD | B. | l⊥AC | ||
| C. | 面MEF与面MPQ垂直 | D. | 当x变化时,l是定直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
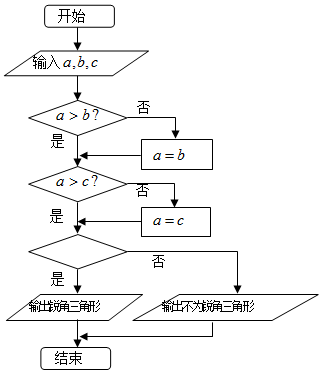 下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )
下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
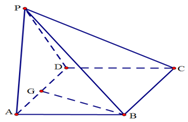 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com