
分析 方法一:设直线的斜率,代入椭圆方程,根据韦达定理及中点坐标公式,即可求得直线的斜率,求得直线方程;
方法二:设弦的两端点坐标为(x1,y1)、(x2,y2),代入椭圆方程,作差,即可求得直线的斜率,求得的直线方程;
方法三:设过P的弦与椭圆相交于M(1+m,1+n),N(1-m,1-n),代入椭圆方程,作差,即可求得m+2n=0,则直线k=$\frac{n}{m}$=-$\frac{1}{2}$,求得的直线方程;
解答 解:解法一:易知引弦所在直线的斜率存在,则设其方程为y-1=k(x-1),
弦的两端点为(x1,y1),(x2,y2).
由$\left\{\begin{array}{l}{y-1=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去y得(2k2+1)x2-4k(k-1)x+2(k2-2k-1)=0,
∴x1+x2=$\frac{4k(k-1)}{2{k}^{2}+1}$.
又∵x1+x2=2,∴$\frac{4k(k-1)}{2{k}^{2}+1}$=2,得k=-$\frac{1}{2}$.
故弦所在直线方程为y-1=-$\frac{1}{2}$(x-1),即x+2y-3=0.
解法二:由于此弦所在直线的斜率存在,所以设斜率为k,且设弦的两端点坐标为(x1,y1)、(x2,y2),
则$\frac{{x}_{1}^{2}}{4}$+$\frac{{y}_{1}^{2}}{2}$=1,$\frac{{x}_{2}^{2}}{4}$+$\frac{{y}_{2}^{2}}{2}$=1,两式相减得
$\frac{({x}_{1}+{x}_{2})({x}_{1}-{x}_{2})}{4}$+$\frac{({y}_{1}+{y}_{2})({y}_{1}-{y}_{2})}{2}$=0.
∵x1+x2=2,y1+y2=2,
∴$\frac{x1-x2}{2}$+(y1-y2)=0,
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{2}$.
∴此弦所在直线方程为y-1=-$\frac{1}{2}$(x-1),即x+2y-3=0.
∴此弦所在的直线方程x+2y-3=0.
方法三:由题意可知:过P的弦与椭圆相交于M(1+m,1+n),N(1-m,1-n),
由M,N在椭圆方程:$\frac{(1+m)^{2}}{4}+\frac{(1+n)^{2}}{2}=1$,$\frac{(1-m)^{2}}{4}+\frac{(1-n)^{2}}{2}=1$,
两式相减得:m+2n=0,
则直线MN的斜率k=$\frac{(1+n)-(1-n)}{(1+m)-(1-m)}$=$\frac{n}{m}$=-$\frac{1}{2}$,
此弦所在直线方程为y-1=-$\frac{1}{2}$(x-1),即x+2y-3=0.
点评 本题考查直线与椭圆的位置关系,考查直线的点斜式方程,点差法的应用,方法多,注意灵活应用,考查计算能力,属于中档题.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| y(万盒) | 4 | 4 | 5 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
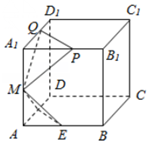 已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )| A. | l∥面ABCD | B. | l⊥AC | ||
| C. | 面MEF与面MPQ垂直 | D. | 当x变化时,l是定直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com