
| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
分析 根据等差数列{an}的前n项和公式,利用项的性质,列出不等式组,求出a7>0,a8<0,即得k的值.
解答 解:根据题意,S13>0,S14<0,
得$\left\{\begin{array}{l}{\frac{13({a}_{1}+{a}_{13})}{2}>0}\\{\frac{14({a}_{1}+{a}_{14})}{2}<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{{a}_{1}+{a}_{13}>0}\\{{a}_{1}+{a}_{14}<0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{a}_{1}+{a}_{13}=2{a}_{7}>0}\\{{a}_{1}+{a}_{14}={a}_{7}+{a}_{8}<0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{a}_{7}>0}\\{{a}_{8}<0}\end{array}\right.$;
又ak•ak+1<0,
∴k=7.
故选:B.
点评 本题考查了等差数列{an}的前n项和公式与项的性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| y(万盒) | 4 | 4 | 5 | 6 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
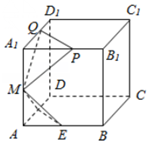 已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )
已知棱长为l的正方体ABCD-A1B1C1D1中,E,F,M分别是AB、AD、AA1的中点,又P、Q分别在线段A1B1,A1D1上,且A1P=A1Q=x,0<x<1,设面MEF∩面MPQ=l,则下列结论中不成立的是( )| A. | l∥面ABCD | B. | l⊥AC | ||
| C. | 面MEF与面MPQ垂直 | D. | 当x变化时,l是定直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com