练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．在Rt△ABC中，∠C=90°，$\overrightarrow{AB}=（1，x），\overrightarrow{AC}=（-1，2）$，则实数x=3．

    分析 由题意和向量的坐标运算求出$\overrightarrow{CB}$的坐标，由条件和向量垂直的坐标条件列出方程，求出x的值．

    解答 解：∵$\overrightarrow{AB}=（1，x），\overrightarrow{AC}=（-1，2）$，
    ∴$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}=（2，x-2）$，
    ∵在Rt△ABC中，∠C=90°，
    ∴$\overrightarrow{AC}•\overrightarrow{CB}=0$，则-2+2（x-2）=0，
    解得x=3，
    故答案为：3．

    点评 本题考查向量的坐标运算，以及向量垂直的坐标条件的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知边长为2的正方形ABCD的四个顶点在球O的球面上，球O的体积为V球=$\frac{160\sqrt{5}π}{3}$，则OA与平面ABCD所成的角的余弦值为$\frac{\sqrt{10}}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．定义：若存在实数x1∈[-2，-1]，x2∈[a，32]使2${\;}^{-{x}_{1}}$=log2x2成立，则称a为指对实数，那么在a∈[-20，20]上成为指对实数的概率是$\frac{9}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．定义在R上的函数y=f（x），当x∈[0，2]时，f（x）=4（1-|x-1|），且对任意实数x∈[2n-2，2n+1-2]（n∈N*，n≥2），都有f（x）=$\frac{1}{2}$f（$\frac{x}{2}$-1）．若g（x）=f（x）-logax有且仅有3个零点，则实数a的取值范围是（　　）
    A．[2，10]B．[$\sqrt{2}$，$\sqrt{10}$]C．（2，10）D．[2，10）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

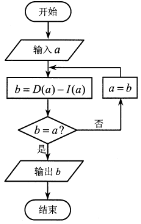    14．设a是一个各位数字都不是0且没有重复数字的三位数，将组成a的3个数字按从小到大排成的三位数记为I（a），按从大到小排成的三位数记为D（a），（例如a=746，
    则I（a）=467，D（a）=764）阅读如右图所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b=495．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．设△ABC的内角A、B、C所对的边分别为a、b、c，若a2sinC=4sinA，cosB=$\frac{\sqrt{7}}{4}$，则△ABC的面积为（　　）
    A．1B．$\frac{3}{2}$C．2D．$\frac{5}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知向量$\overrightarrow{a}$=（sinx，mcosx），$\overrightarrow{b}$=（3，-1）．
    （1）若$\overrightarrow{a}$∥$\overrightarrow{b}$，且m=1，求2sin2x-3cos2x的值；
    （2）若函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$的图象关于直线x=$\frac{2π}{3}$对称，求函数f（2x）在[$\frac{π}{8}$，$\frac{2π}{3}$]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．若数列{an}是公差为2的等差数列，数列{bn}满足b1=1，b2=2且anbn+bn=nbn+1．
    （1）求数列{an}、{bn}的通项公式；
    （2）设数列{cn}满足cn=$\frac{{a}_{n}+1}{{b}_{n+1}}$，数列{cn}的前n项和为Tn，则Tn＜4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知球O的半径为13，其球面上有三点A、B、C，若AB=12$\sqrt{3}$，AC=BC=12，则四面体OABC的体积是60$\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案