Question

【题目】在极坐标系中，直线l的极坐标方程为ρcos（θ+ ）=1．以极点O为原点，极轴为x轴的正半轴建立平面直角坐标系，圆C的参数方程为 （θ为参数）．若直线l与圆C相切，求r的值．

Answer 1

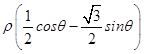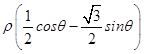【答案】解：由直线l的极坐标方程为ρcos（θ+ ）=1．展开可得： =1，可得： 由直线l的极坐标方程为ρcos（θ+ ）=1．展开可得： =1，利用互化公式可得直线l的直角坐标方程．C的参数方程为 （θ为参数）．利用平方关系可得：圆C的直角坐标方程为：x2+y2=r2 ． 利用直线和曲线相切的性质即可得出．
直线l的直角坐标方程为x﹣ y﹣2=0，
圆C的参数方程为 （θ为参数）．
圆C的直角坐标方程为：x2+y2=r2 ．
则直线和曲线相切，得r= 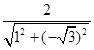=1
【解析】由直线l的极坐标方程为ρcos（θ+ ）=1．展开可得： =1，利用互化公式可得直线l的直角坐标方程．C的参数方程为 （θ为参数）．利用平方关系可得：圆C的直角坐标方程为：x2+y2=r2 ． 利用直线和曲线相切的性质即可得出