
已知函数 ,
,
(1)判断函数 的奇偶性; (2)求函数
的奇偶性; (2)求函数 的单调区间;
的单调区间;
(3)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围.
的取值范围.
(1)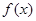 为偶函数
为偶函数
(2)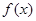 的递增区间是
的递增区间是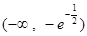 和
和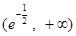 ;递减区间是
;递减区间是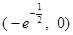 和
和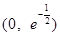 .
.
(3)(-∞,-1]∪[1,+∞)
【解析】本试题主要考查而来函数的奇偶性和周期性和单调性以及方程的解的综合运用。
(1)函数f(x)的定义域为 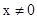 ,然后利用定义判定
,然后利用定义判定
∴f(x)为偶函数
(2)当x>0时,求解导函数,讨论得到单调区间,进而的分析最值
(3))利用由f(x)=kx-1, 构造函数利用导数得到结论。
解:(1)函数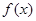 的定义域为{
的定义域为{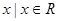 且
且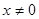 }
}
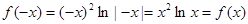 ∴
∴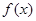 为偶函数
为偶函数
(2)当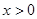 时,
时,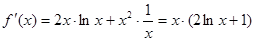
若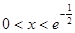 ,则
,则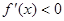 ,
,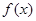 递减;
递减;
若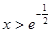 , 则
, 则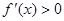 ,
,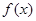 递增.
递增.
再由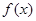 是偶函数,
是偶函数,
得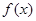 的递增区间是
的递增区间是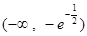 和
和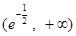 ;
;
递减区间是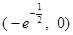 和
和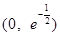 .
.
(3)由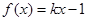 ,得:
,得: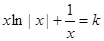 令
令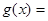

当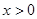 ,
,
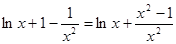 显然
显然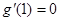
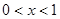 时,
时,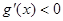 ,
,
 时,
时,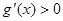 ,
,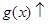
∴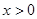 时,
时,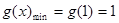
又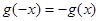 ,
,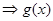 为奇函数 ∴
为奇函数 ∴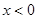 时,
时,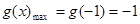
∴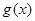 的值域为(-∞,-1]∪[1,+∞)
的值域为(-∞,-1]∪[1,+∞)
∴若方程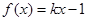 有实数解,则实数
有实数解,则实数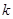 的取值范围是(-∞,-1]∪[1,+∞).
的取值范围是(-∞,-1]∪[1,+∞).


科目:高中数学 来源: 题型:

 (理)已知函数f(x)=
(理)已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-xp |
| 1+λxp |
| 1 |
| p |
| 1 |
| n |
| n |
 |
| i=1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(江西卷解析版) 题型:解答题
若函数h(x)满足
(1)h(0)=1,h(1)=0;
(2)对任意 ,有h(h(a))=a;
,有h(h(a))=a;
(3)在(0,1)上单调递减。则称h(x)为补函数。已知函数
(1)判函数h(x)是否为补函数,并证明你的结论;
(2)若存在 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围;
(3)当 =0,
=0, 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

 (理)已知函数
(理)已知函数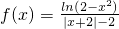 .
.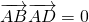 ,求D2+E2-4F的值;
,求D2+E2-4F的值;查看答案和解析>>
科目:高中数学 来源:2011年上海市普陀区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
 .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com