Question

3．设f（x）=-2ln（x+1）+$\frac{1}{2}$x²-a（x-2）（a∈R）．
（1）当a=0时，求f（x）的单调区间和极值；
（2）若存在唯一整数x₀使f（x₀）＜0，求a的取值范围．

Answer 1

分析 （1）把a=0代入函数解析式，求出函数的导函数，由导函数的零点对定义域分段，利用导函数在各区间段内的符号可得函数单调性，从而求得极值；
（2）存在唯一整数x₀使f（x₀）＜0，即存在唯一整数x₀使$-2ln（{x}_{0}+1）+\frac{1}{2}{{x}_{0}}^{2}-a（{x}_{0}-2）$＜0，也就是a（x₀-2）＞$-2ln（{x}_{0}+1）+\frac{1}{2}{{x}_{0}}^{2}$，令g（x）=-2ln（x+1）+$\frac{1}{2}{x}^{2}$，h（x）=a（x-2），结合（1）作出函数图象，数形结合得答案．

解答 解：（1）当a=0时，f（x）=-2ln（x+1）+$\frac{1}{2}$x²，
f′（x）=-$\frac{2}{x+1}+x=\frac{{x}^{2}+x-2}{x+1}$=$\frac{（x+2）（x-1）}{x+1}$（x＞-1），
∴当x∈（-1，1）时，f′（x）＜0，f（x）为减函数，
当x∈（1，+∞）时，f′（x）＞0，f（x）为增函数，
∴当x=1时，函数f（x）求得极小值为f（1）=$-ln2+\frac{1}{2}$；
（2）存在唯一整数x₀使f（x₀）＜0，
即存在唯一整数x₀使$-2ln（{x}_{0}+1）+\frac{1}{2}{{x}_{0}}^{2}-a（{x}_{0}-2）$＜0，
也就是a（x₀-2）＞$-2ln（{x}_{0}+1）+\frac{1}{2}{{x}_{0}}^{2}$，
令g（x）=-2ln（x+1）+$\frac{1}{2}{x}^{2}$，h（x）=a（x-2）．
由（1）可知，x∈（-1，1）时，g（x）为减函数，
当x∈（1，+∞）时，g（x）为增函数，且极小值为$-ln2+\frac{1}{2}$．
∵ln（x+1）＜x（x＞0），∴g（x）=-2ln（x+1）+$\frac{1}{2}{x}^{2}$＞$\frac{1}{2}{x}^{2}+2x$，
作出函数g（x）与h（x）的图象如图：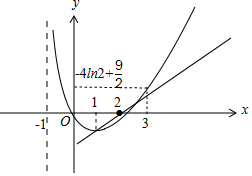

要使存在唯一整数x₀使f（x₀）＜0，则$\left\{\begin{array}{l}{-a≤-ln2+\frac{1}{2}}\\{a≤-4ln2+\frac{9}{2}}\end{array}\right.$，则ln2-$\frac{1}{2}≤a≤$-4ln2+$\frac{9}{2}$．
∴a的取值范围是ln2-$\frac{1}{2}≤a≤$-4ln2+$\frac{9}{2}$．

点评 本题考查利用导数研究函数的单调性，考查数学转化思想方法和数形结合的解题思想方法，属难题．