
已知a≥0,函数f(x)=(x2-2ax)ex,若f(x)在[-1,1]上是单调减函数,则a的取值范围是( )
A.0<a<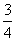 B.
B.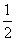 <a<
<a<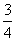
C.a≥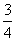 D.0<a<
D.0<a<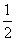
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB中点,且△PMB为正三角形.
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的函数g(x)及二次函数h(x)满足:g(x)+2g(-x)=ex+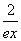 -9,h(-2)=h(0)=1且h(-3)=-2.
-9,h(-2)=h(0)=1且h(-3)=-2.
(1)求g(x)和h(x)的解析式;
(2)对于x1,x2∈[-1,1],均有h(x1)+ax1+5≥g(x2)-x2g(x2)成立,求a的取值范围;
(3)设f(x)=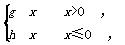 在(2)的条件下,讨论方程f[f(x)]=a+5的解的个数情况.
在(2)的条件下,讨论方程f[f(x)]=a+5的解的个数情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=a1且bn=an+bn-1(n≥2,n∈N*),求数列{bn}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com