
分析 (1)求解f'(x)=1-aeax,分类讨论判断单调性.
(2)利用因为$f(x)≥f(\frac{2}{a})$,所以$f(\frac{2}{a})$是f(x)的最小值,利用导数讨论得出f(x)增区间为$(-∞,\frac{1}{a}ln\frac{1}{a})$,减区间$(\frac{1}{a}ln\frac{1}{a},+∞)$,利用最值得出以$\frac{1}{a}ln\frac{1}{a}≤\frac{1}{a}$或$\left\{\begin{array}{l}\frac{1}{a}<\frac{1}{a}ln\frac{1}{a}<\frac{2}{a}\\ f(\frac{1}{a})≥f(\frac{2}{a})\end{array}\right.$.
(3)分类讨论根据单调性得出最小值,①当a≤0时,f(-1)<f(0)=0成立;当0<a≤1时,f(-1)<f(0)=0成立;当a>1时,f(1)<f(0)=0成立;判断存在问题的成立.
解答 解:(1)f'(x)=1-aeax
①当a≤0时,f'(x)=1-aeax>0,所以f(x)的增区间为(-∞,+∞)
②当a>0时,f'(x)=1-aeax>0,解得$x<\frac{1}{a}ln\frac{1}{a}$,f(x)的增区间为$(-∞,\frac{1}{a}ln\frac{1}{a})$,减区间$(\frac{1}{a}ln\frac{1}{a},+∞)$
(2)因为$f(x)≥f(\frac{2}{a})$,所以$f(\frac{2}{a})$是f(x)的最小值,由题意a>0,
由(1)f(x)增区间为$(-∞,\frac{1}{a}ln\frac{1}{a})$,减区间$(\frac{1}{a}ln\frac{1}{a},+∞)$
所以$\frac{1}{a}ln\frac{1}{a}≤\frac{1}{a}$或$\left\{\begin{array}{l}\frac{1}{a}<\frac{1}{a}ln\frac{1}{a}<\frac{2}{a}\\ f(\frac{1}{a})≥f(\frac{2}{a})\end{array}\right.$,解得$a≥\frac{1}{{{e^2}-e}}$
(3)因为f(0)=0
①当a≤0时,f(x)在R单调递增,所以存在t=-1,f(-1)<f(0)=0成立;
②当0<a≤1时,$\frac{1}{a}ln\frac{1}{a}≥0$f(x)在[-1,0]上递增,所以存在t=-1,f(-1)<f(0)=0成立;
③当a>1时,$\frac{1}{a}ln\frac{1}{a}<0$,f(x)在[0,1]上递减,所以存在t=1,f(1)<f(0)=0成立;
综上,总存在t∈[-1,1],使得f(t)<0.
点评 本题综合考查了导数的运用,学生的综合分析问题的能力,解决问题的能力,属于综合题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
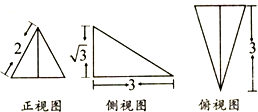
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 3$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
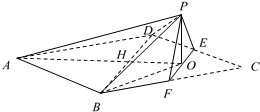 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com