
| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | 4 |
分析 根据球体体积计算球的半径,得出底面直角三角形的斜边长,从而得出底面直角边a,b的关系,利用基本不等式求得ab的最大值,代入棱柱的体积得出体积的最大值.
解答 解:设三棱柱底面直角三角形的直角边为a,b则棱柱的高h=$\sqrt{{a}^{2}+{b}^{2}}$,
设外接球的半径为r,则4πr2=8π,解得r=$\sqrt{2}$,
∵正方形的中心是该三棱柱的外接球的球心,∴$\sqrt{2}$h=2r=2$\sqrt{2}$.
∴h=2,
∴a2+b2=h2=4≥2ab,∴ab≤2.
∴三棱柱的体积V=Sh=$\frac{1}{2}$abh=ab≤2.
故选:A.
点评 本题考查了棱柱与外接球的关系,求出底面直角边的关系是关键,属于中档题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
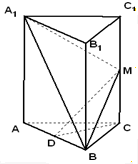 在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM
在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (e,+∞) | B. | (-∞,e) | C. | (-∞,$\frac{1}{e}$) | D. | [0,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com