
分析 设M(m,n)到抛物线y2=2x的准线x=-$\frac{1}{2}$的距离等于d,由抛物线的定义可得$\frac{|MO|}{|MF|}$=$\frac{\sqrt{{m}^{2}+{n}^{2}}}{m+\frac{1}{2}}$=$\sqrt{1+\frac{m-\frac{1}{4}}{{m}^{2}+m+\frac{1}{4}}}$,令m-$\frac{1}{4}$=t,利用基本不等式可求得最大值.
解答 解:焦点F($\frac{1}{2}$,0),设M(m,n),则n2=2m,m>0,设M到准线x=-$\frac{1}{2}$的距离等于d,
则由抛物线的定义得$\frac{|MO|}{|MF|}$=$\frac{\sqrt{{m}^{2}+{n}^{2}}}{m+\frac{1}{2}}$=$\sqrt{1+\frac{m-\frac{1}{4}}{{m}^{2}+m+\frac{1}{4}}}$,
令m-$\frac{1}{4}$=t,
依题意知,m>0,
若t>0,
则$\frac{m-\frac{1}{4}}{{m}^{2}+m+\frac{1}{4}}$=$\frac{t}{{t}^{2}+\frac{3}{2}t+\frac{9}{16}}$=$\frac{1}{t+\frac{\frac{9}{16}}{t}+\frac{3}{2}}$≤$\frac{1}{3}$,
∴tmax=$\frac{1}{3}$,此时($\frac{|MO|}{|MF|}$)max=$\sqrt{1+\frac{1}{3}}$=$\frac{2\sqrt{3}}{3}$;
若-$\frac{1}{4}$<t<0,y=t+$\frac{\frac{9}{16}}{t}$+$\frac{3}{2}$单调递减,故y<-1,$\frac{1}{y}$∈(-1,0);
综上所述,($\frac{|MO|}{|MF|}$)max=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查抛物线的定义、简单性质,基本不等式的应用,体现了换元的思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | (-10,-6) | B. | [-12,-2) | C. | [-12,-6) | D. | [-12,-10) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
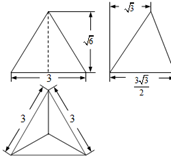
| A. | $\frac{{9\sqrt{3}}}{4}$ | B. | $9\sqrt{3}$ | C. | $\frac{{9\sqrt{2}}}{4}$ | D. | $9\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:填空题
在映射 中,如果
中,如果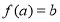 ,那么称
,那么称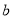 为
为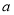 的像.设
的像.设 ,
, 使
使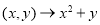 ,则
,则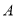 中所有元素的像构成的集合是______.(用列举法表示)
中所有元素的像构成的集合是______.(用列举法表示)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com