
���� ��1������ֱ��l����P��2��6��������б��Ϊ$\frac{3��}{4}$���ɵ�ֱ��l�IJ������̣���$��=20sin��\frac{��}{4}-\frac{��}{2}��cos��\frac{��}{4}-\frac{��}{2}��$�æ�=10cos�ȣ�����2=10��cos�ȣ�l���û�����ʽ���ɵó�����C��ֱ�����귽�̣�
��2����l�IJ������̴���ԲC��ֱ�����귽�̣���${t^2}+9\sqrt{2}t+20=0$������0������|PA|+|PB|=|t1+t2|���ɵó���
��� �⣺��1����ֱ��l����P��2��6��������б��Ϊ$\frac{3��}{4}$��
��ֱ��l�IJ�������Ϊ$\left\{{\begin{array}{l}{x=2-\frac{{\sqrt{2}}}{2}t}\\{y=6+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$��tΪ��������
��$��=20sin��\frac{��}{4}-\frac{��}{2}��cos��\frac{��}{4}-\frac{��}{2}��$�æ�=10cos�ȣ�����2=10��cos�ȣ�
������C��ֱ�����귽��Ϊx2+y2-10x=0��
��2����l�IJ������̴���ԲC��ֱ�����귽�̣�
��${��-3-\frac{{\sqrt{2}}}{2}t��^2}+{��6+\frac{{\sqrt{2}}}{2}t��^2}=25$��${t^2}+9\sqrt{2}t+20=0$����=82��0��
������t1��t2�������̵�����ʵ��������$\left\{{\begin{array}{l}{{t_1}+{t_2}=-9\sqrt{2}}\\{{t_1}{t_2}=20}\end{array}}\right.$��
��ֱ��l����P��2��6��������$|{PA}|+|{PB}|=|{t_1}|+|{t_2}|=|{{t_1}+{t_2}}|=9\sqrt{2}$��
���� ���⿼����ֱ�߲������̵�Ӧ�á������귽�̻�Ϊֱ�����귽�̡�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��������������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�갲������һ�и�һ�Ϲ�����ҵ����ѧ�Ծ��������棩 ���ͣ������
��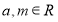 ��
��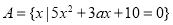 ��
��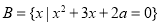 ��
��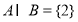 ��
��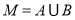 .
.
��1����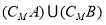 ��
��
��2����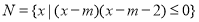 ����
����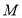 �����ҽ���2��Ԫ������
�����ҽ���2��Ԫ������ ����
���� ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
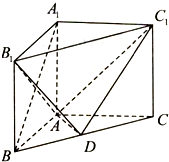 ��ͼ����ֱ������ABC-A1B1C1�У���D��BC���е㣬AB��AC��AB=AC=AA1=2��
��ͼ����ֱ������ABC-A1B1C1�У���D��BC���е㣬AB��AC��AB=AC=AA1=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������f��x����ͼ����P�㴦�����߷�����y=-2x+17������P�ĺ�������5����f��5��+f�䣨5��=��������
��ͼ������f��x����ͼ����P�㴦�����߷�����y=-2x+17������P�ĺ�������5����f��5��+f�䣨5��=��������| A�� | 5 | B�� | -5 | C�� | 10 | D�� | -10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
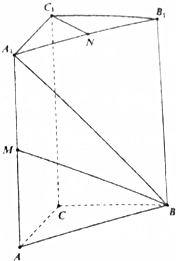 ��ͼ��ʾ����ֱ������ABC-A1B1C1�У���֪CA��CB��CA=CB=1��AA1=2������AA1��A1B1���е�ֱ���M��N��
��ͼ��ʾ����ֱ������ABC-A1B1C1�У���֪CA��CB��CA=CB=1��AA1=2������AA1��A1B1���е�ֱ���M��N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
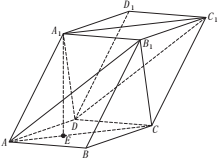 ��ͼ������ABCD-A1B1C1D1�ĵ��������Σ����ⳤΪ5��ƽ��ABCD��ƽ��A1ACC1��AB=3$\sqrt{3}$����BAD=60�㣬��E�ǡ�ABD�����ģ���A1E=4��
��ͼ������ABCD-A1B1C1D1�ĵ��������Σ����ⳤΪ5��ƽ��ABCD��ƽ��A1ACC1��AB=3$\sqrt{3}$����BAD=60�㣬��E�ǡ�ABD�����ģ���A1E=4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com