
分析 (Ⅰ)a=6时便可得出x满足:|x+1|+|x-1|<3,讨论x,从而去掉绝对值符号,这样便可求出每种情况x的范围,可得不等式的解集;
(Ⅱ)由二次函数y=x2+2x+3=(x+1)2+2在x=-1取得最小值2,f(x)在x=-1处取得最大值a-2,故有a-2≥2,由此求得m的范围.
解答 解:(Ⅰ)由题设知:6-|x-1|-|x+1|>3.
|x+1|+|x-1|<3;
①当x>1时,得x+1+x-1<3,解得x<$\frac{3}{2}$;
②当-1≤x≤1时,得x+1+1-x<3,恒成立;
③当x<-1时,得-x-1-x+1<3,解得x>-$\frac{3}{2}$;
∴不等式的解集为:(-$\frac{3}{2}$,$\frac{3}{2}$);
解:由二次函数y=x2+2x+3=(x+1)2+2,该函数在x=-1取得最小值2,
因为f(x)=a-|x-1|-|x+1|.
f(x)=$\left\{\begin{array}{l}{2x+a,x<-1}\\{a-2,-1≤x≤1}\\{a-2x,x>1}\end{array}\right.$,在x=-1处取得最大值a-2,
所以要使二次函数y=x2+2x+3与函数y=f(x)的图象恒有公共点,只需a-2≥2,
求得a≥4.
点评 本题主要考查了函数的恒成立问题,绝对值不等式的解法,二次函数的性质,体现了转化的数学思想,属于中档题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
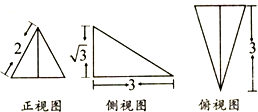
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | 3$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
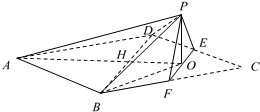 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com