
分析 根据题意,得出△ABC为锐角三角形时x2+y2>1;
再由三角形的两边和大于第三边,得出x+y>1;
由此求出对应图形的面积比即可得出概率值.
解答 解:△ABC的三边为x、y、1,且x、y∈(0,1);
△ABC为锐角三角形,则x2+y2>1,且x+y>1;
画出图象,如图所示;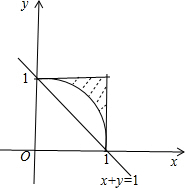
在曲线x2+y2=1之外的区域与正方形重合的阴影部分,
构成三角形的区域为不等式x+y>1表示的区域和正方形区域的重合部分,
∴S阴影=1-$\frac{1}{4}$π×12=1-$\frac{π}{4}$,
三角形面积为$\frac{1}{2}$×1×1=$\frac{1}{2}$;
所求的概率值为P=$\frac{{S}_{阴影}}{{S}_{三角形}}$=$\frac{1-\frac{π}{4}}{\frac{1}{2}}$=2-$\frac{π}{2}$.
故答案为:2-$\frac{π}{2}$.
点评 本题考查了几何概型的概率计算问题,是综合性题目.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
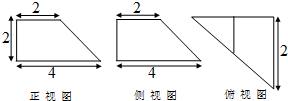 已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图和侧视图为全等的直角梯形,俯视图为直角三角形则该几何体的表面积为( )| A. | 6+12$\sqrt{2}$ | B. | 16+12$\sqrt{2}$ | C. | 6+12$\sqrt{3}$ | D. | 16+12$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
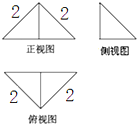 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )| A. | 2$\sqrt{3}$+4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 2$\sqrt{3}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{e_1}$,2$\overrightarrow{e_2}$ | B. | $\overrightarrow{e_1}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | ||
| C. | -$\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | D. | $\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若θ=90°,则直线PB与平面BCD所成角大小为45° | |
| B. | 若直线PB与平面BCD所成角大小为45°,则θ=90° | |
| C. | 若θ=60°,则直线BD与PC所成角大小为90° | |
| D. | 若直线BD与PC所成角大小为90°,则θ=60° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
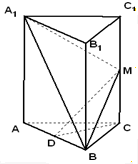 在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM
在直三棱柱ABC-A1B1C1中,底面ABC为等边三角形,且AA1=2AB,D、M 分别为AB,CC1的中点,求证:(1)CD∥平面A1BM查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com