
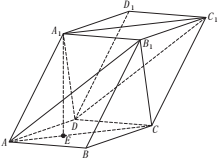
 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.分析 (1)推导出四边形A1ACC1是平行四边形,从而A1C1∥AC.进而四边形ADC1B1是平行四边形,从而AB1∥DC1,进而AC∥平面A1DC1,AB1∥平面A1DC1,由此能证明平面A1DC1∥平面AB1C.
(2)设AC∩BD=O,推导出A1E⊥AC,从而A1E⊥平面ABCD.以E为原点,分别以AC,A1E所在直线为x,z轴,以过点E与BD平行的直线为y轴建立空间直角坐标系,利用向量法能求出二面角B1-AC-B的余弦值.
解答 证明:(1)因为AA1平行等于CC1,所以四边形A1ACC1是平行四边形,所以A1C1∥AC.
又因为AD平行等于B1C1,所以四边形ADC1B1是平行四边形,所以AB1∥DC1.
因为AC,AB1?平面A1DC1,A1C1,DC1⊆平面A1DC1,
所以AC∥平面A1DC1,AB1∥平面A1DC1,又因为AC∩AB1=A,AC,AB1⊆平面AB1C,
所以平面A1DC1∥平面AB1C.
解:(2)设AC∩BD=O,由题意可知△ABD是等边三角形.
因为$AB=3\sqrt{3}$,所以$OA=ABcos∠BAC=3\sqrt{3}cos{30°}=\frac{9}{2}$,
所以$AE=\frac{2}{3}OA=3$,所以$AA_1^2={A_1}{E^2}+A{E^2}$,所以A1E⊥AC,
又因为平面ABCD⊥平面A1ACC1,平面ABCD∩平面A1ACC1=AC,A1E⊆平面A1ACC1,所以A1E⊥平面ABCD.
以E为原点,分别以AC,A1E所在直线为x,z轴,以过点E与BD平行的直线为y轴建立空间直角坐标系,
则$E(0,0,0),{A_1}(0,0,4),A(-3,0,0),B(\frac{3}{2},-\frac{{3\sqrt{3}}}{2},0),C(6,0,0)$.设B1(x1,y1,z1).
因为$\overrightarrow{A{A_1}}=(3,0,4)$,$\overrightarrow{B{B_1}}=({x_1}-\frac{3}{2},{y_1}+\frac{{3\sqrt{3}}}{2},{z_1})$,$\overrightarrow{A{A_1}}=\overrightarrow{B{B_1}}$,所以$\overrightarrow{B{B_1}}=(\frac{9}{2},-\frac{{3\sqrt{3}}}{2},4)$.
由A1E⊥平面ABCD,可知平面ABCD的法向量是$\overrightarrow{E{A_1}}=(0,0,4)$.
设平面B1AC的法向量是$\overrightarrow n=(x,y,z)$,而$\overrightarrow{AC}=(9,0,0)$,$\overrightarrow{A{B_1}}=(\frac{15}{2},-\frac{{3\sqrt{3}}}{2},4)$.
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AC}=9x=0}\\{\overrightarrow n•\overrightarrow{A{B_1}}=\frac{15}{2}x-\frac{{3\sqrt{3}}}{2}y+4z=0}\end{array}}\right.$,所以$x=0,z=\frac{{3\sqrt{3}}}{8}y$.
所以$\overrightarrow n=(0,y,\frac{{3\sqrt{3}}}{8}y)=\frac{1}{8}y(0,8,3\sqrt{3})$.
取平面B1AC的法向量$\overrightarrow n=(0,8,3\sqrt{3})$,所以$cos<\overrightarrow{E{A_1}},\overrightarrow n>=\frac{{\overrightarrow{E{A_1}}•\overrightarrow n}}{{|{\overrightarrow{E{A_1}}}||{\overrightarrow n}|}}=\frac{{3\sqrt{273}}}{91}$.
故二面角B1-AC-B的余弦值为$\frac{3\sqrt{273}}{91}$.
点评 本题考查面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{9\sqrt{3}}}{4}$ | B. | $9\sqrt{3}$ | C. | $\frac{{9\sqrt{2}}}{4}$ | D. | $9\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:填空题
在映射 中,如果
中,如果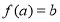 ,那么称
,那么称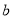 为
为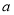 的像.设
的像.设 ,
, 使
使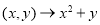 ,则
,则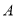 中所有元素的像构成的集合是______.(用列举法表示)
中所有元素的像构成的集合是______.(用列举法表示)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
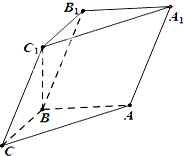 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高一上国庆作业二数学试卷(解析版) 题型:选择题
已知函数 的定义域为
的定义域为 ,值域为
,值域为 ,那么满足条件的整数对
,那么满足条件的整数对 共有( )
共有( )
A.6个 B.7个
C.8个 D.9个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com