
分析 (1)分类讨论,a=0时显然符合题意,a>0时,构造函数,根据导数和函数的最值的关系即可求出a的取值范围;
(2)所求证式子可化为${e^{\frac{1}{e}x}}>eln(x-e)+e(x>e)$,构造函数r(x)=eln(x-e)+e(x>e),求导,根据导数和函数的最值的关系,以及(1)的结论即可证明.
解答 解:(1)a=0时显然符合题意,
a>0时,因为f($\frac{1}{e}$x)-ax≥0恒成立,即${e}^{\frac{1}{e}x}$-ax≥0,恒成立,
令h(x)=${e}^{\frac{1}{e}x}$-ax,
则$h'(x)=\frac{1}{e}{e^{\frac{1}{e}x}}-a$,
假设h'(x0)=0,则${e^{\frac{1}{e}{x_0}}}=ae,{x_0}=e(lna+1)$,
且可知x∈(-∞,x0)时h'(x0)<0,x∈(x0,+∞)时h'(x0)>0,
所以h(x)≥h(x0),令h(x0)>0,得ae-ae(lna+1)≥0,
所以lna≤0,
所以0≤a≤1.
(2)证明:所求证式子可化为${e^{\frac{1}{e}x}}>eln(x-e)+e(x>e)$,
令r(x)=eln(x-e)+e(x>e),则$r'(x)=\frac{e}{x-e}-1=\frac{2e-x}{x-e}(x>e)$,
易得x=2e时r(x)有最大值,而r(2e)=elne+e-2e=0,
所以r(x)≤0且x=2e时取“=”,
即x≥eln(x-e)+e且x=2e时取“=”,
由(1)可知${e^{\frac{1}{e}x}}≥x$且x=x0=e时取“=”,
所以${e^{\frac{1}{e}x}}≥eln(e-x)+e$,
即$f(\frac{1}{e}x-1)-g(x-e)>1$.
点评 本题考查利用导数求函数的最值,考查了函数恒成立问题,考查了数学转化思想方法和分类讨论的数学思想方法,属难题.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
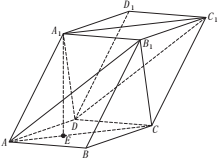 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com