
【题目】设![]() 为数列
为数列![]() 的前
的前![]() 项和,对任意的
项和,对任意的![]() ,都有
,都有![]() (
(![]() 为正常数).
为正常数).
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)利用![]() 与
与![]() 之间的关系
之间的关系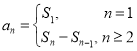 ,对
,对![]() 分两种情况讨论,
分两种情况讨论,![]() 时,求
时,求![]() 的值,
的值,![]() 时,利用
时,利用![]() 得出
得出![]() 与
与![]() 之间的关系,进而利用定义证明数列
之间的关系,进而利用定义证明数列![]() 为等比数列;
为等比数列;
(2)在(1)的条件下求出![]() 的值,然后根据数列
的值,然后根据数列![]() 的递推公式的结构利用倒数法得到数列
的递推公式的结构利用倒数法得到数列![]() 为等差数列,通过求处等差数列
为等差数列,通过求处等差数列![]() 的通项公式求出数列
的通项公式求出数列![]() 的通项公式;(3)利用(2)中数列
的通项公式;(3)利用(2)中数列![]() 的通项公式,并根据数列
的通项公式,并根据数列![]() 的通项公式的结构选择错位相减法求数列
的通项公式的结构选择错位相减法求数列![]() 的前
的前![]() 项和
项和![]() .
.
试题解析:(1)证明:当![]() 时,
时,![]() ,解得
,解得![]() . 1分
. 1分
当![]() 时,
时,![]() .即
.即![]() . 2分
. 2分
又![]() 为常数,且
为常数,且![]() ,∴
,∴![]() . 3分
. 3分
∴数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列. 4分
的等比数列. 4分
(2)![]() 5分 ∵
5分 ∵![]() ,∴
,∴![]()
![]() ,即
,即![]() . 7分
. 7分
∴![]() 是首项为
是首项为![]() ,公差为1的等差数列. 8分
,公差为1的等差数列. 8分
∴![]() ,即
,即![]() . 9分
. 9分
(3)由(2)知![]() ,则
,则![]() .
.
所以![]() , 10分
, 10分
即![]() , ① 11分
, ① 11分
则![]() , ② 12分
, ② 12分
②-①得![]() , 13分
, 13分
故![]() . 14分
. 14分


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】(1)求过直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点,且到点P(0,4)的距离为2的直线方程.
(2)设直线l的方程为(a+1)x+y+2-a=0(a∈R).若l在两坐标轴上的截距相等,求l的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为![]() ,再由乙猜甲刚才想的数字把乙想的数字记为
,再由乙猜甲刚才想的数字把乙想的数字记为![]() ,且
,且![]() ,
, ![]() ,记
,记![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为l的正方体![]() 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、![]() 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段![]() 上,且
上,且![]() ,设面
,设面![]() 面MPQ=
面MPQ=![]() ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A.![]() 面ABCD
面ABCD
B.![]() AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时,![]() 不是定直线
不是定直线
查看答案和解析>>
科目:高中数学 来源: 题型:
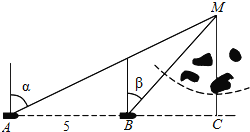
【题目】如图,一船由西向东航行,在A处测得某岛M的方位角为α,前进5km后到达B处,测得岛M的方位角为β.已知该岛周围3km内有暗礁,现该船继续东行.
(1)若α=2β=60°,问该船有无触礁危险?
(2)当α与β满足什么条件时,该船没有触礁的危险?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场预计全年分批购入每台2000元的电视机共3600台.每批都购入![]() 台(
台(![]() 是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
是自然数)且每批均需付运费400元.贮存购入的电视机全年所需付的保管费 与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运输和保管总费用43600元.现在全年只有24000元资金可以支付这笔费用,请问,能否恰当安排每批进货数量,使资金够用?写出你的结论,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com