
【题目】已知函数f(x)=2x的定义域是[0,3],设g(x)=f(2x)﹣f(x+2).
(1)求g(x)的解析式及定义域;
(2)求函数g(x)的最大值和最小值.
【答案】
(1)解:∵f(x)=2x,
∴g(x)=f(2x)﹣f(x+2)=22x﹣2x+2.
因为f(x)的定义域是[0,3],
所以 ![]() ,
,
解之得0≤x≤1.
于是 g(x)的定义域为{x|0≤x≤1}
(2)解:设g(x)=(2x)2﹣4×2x
=(2x﹣2)2﹣4.
∵x∈[0,1],
即2x∈[1,2],
∴当2x=2即x=1时,
g(x)取得最小值﹣4;
当2x=1即x=0时,
g(x)取得最大值﹣3
【解析】(1)由f(x)=2x , 知g(x)=f(2x)﹣f(x+2)=22x﹣2x+2 . 因为f(x)的定义域是[0,3],所以 ![]() ,由此能求出g(x)的定义域.(2)设g(x)=(2x)2﹣4×2x=(2x﹣2)2﹣4.由2x∈[1,2],能求出函数g(x)的最大值和最小值.
,由此能求出g(x)的定义域.(2)设g(x)=(2x)2﹣4×2x=(2x﹣2)2﹣4.由2x∈[1,2],能求出函数g(x)的最大值和最小值.


科目:高中数学 来源: 题型:
【题目】盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球.规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得![]() 分,现从盒内任取3个球.
分,现从盒内任取3个球.
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
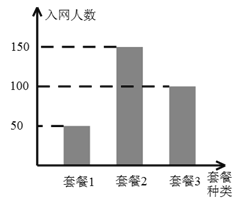
【题目】移动公司在春节正月初八这天推出4G套餐,对这天办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元. 初八当天参与活动的人数统计结果如图所示,
(Ⅰ)从参加当天活动的人中任选一人,求此人获得优惠金额不低于300元的概率(将频率视为概率);
(Ⅱ)若采用分层抽样的方式从参加活动的客户中选出6人,再从该6人中随机选两人,求这两人获得相等优惠金额的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽马鞍山二模】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
轴上截得的弦长为4,记动圆圆心的轨迹为曲线C.
(Ⅰ)求直线![]() 与曲线C围成的区域面积;
与曲线C围成的区域面积;
(Ⅱ)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线C的切线
作曲线C的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产甲,乙两种产品,生产这两种产品每吨需要的煤,电以及每吨产品的产值如表所示.若每天配给该厂的煤至多56吨,供电至多45千瓦,问该厂如何安排生产,使该厂日产值最大?
用煤/吨 | 用电/千瓦 | 产值/万元 | |
甲种产品 | 7 | 2 | 8 |
乙种产品 | 3 | 5 | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若f(log2a)+f(2log ![]() a)≥2f(﹣1),则实数a的取值范围是 .
a)≥2f(﹣1),则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017扬州一模20】已知函数![]() ,其中函数
,其中函数![]() ,
,![]() .
.
(1)求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(3)当![]() 时,对于给定的正整数
时,对于给定的正整数![]() ,问函数
,问函数![]() 是否有零点?请说明理由.(参考数据
是否有零点?请说明理由.(参考数据![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com