练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知三棱锥S－ABC的所有顶点都在球O的球面上，AB＝BC＝CA＝3，SA＝SB＝SC，球心O到平面ABC的距离为1，则SA与平面ABC所成角的大小为(　　)

    A．30°                                 B．60° 

    C．30°或60°                           D．45°或60°


    C

    [解析]　球心位置有以下两种情况：球心在三棱锥内部；球心在三棱锥外部．球心在三棱锥内部时，三棱锥为正三棱锥，设O′为△ABC的中心，在△ABC中，可求得O′A＝，所以可得OA＝2，SO′＝3，SA与平面ABC所成的角即为∠SAO′，由tan ∠SAO′＝＝得，∠SAO′＝60°.同理可得第二种情况中所成角为30°.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若函数f(x)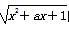＝的定义域为实数集R，则实数a的取值范围为(　　)

    A．(－2,2)   

    B．(－∞，－2)∪(2，＋∞)

    C．(－∞，－2]∪[2，＋∞)   

    D．[－2,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列结论中：

    ①函数y＝x(1－2x)(x>0)有最大值；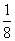

    ②函数y＝2－3x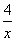－(x<0)有最大值2－4；

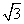    ③若a>0，则(1＋a)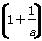≥4.

    正确结论的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


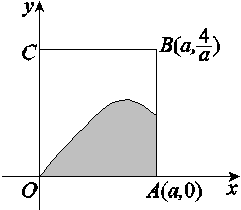
    如图，矩形OABC内的阴影部分由曲线f(x)＝sin x及直线x＝a(a∈(0,2π))与x轴围成．向矩形OABC内随机掷一点，该点落在阴影部分的概率为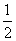，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    前不久，省社科院发布了2013年度“城市居民幸福排行榜”，某市成为本年度城市最“幸福城”．随后，某校学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎，小数点后的一位数字为叶)：

    (1)指出这组数据的众数和中位数；

    (2)若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；

    (3)以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设F1，F2为椭圆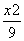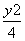＋＝1的两个焦点，P为椭圆上一点，已知P，F1，F2是一个直角三角形的三个顶点，且|PF1|>|PF2|，则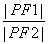的值为(　　)

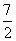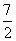    A．2  B.  C．2或  D．3或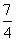

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设等差数列{an}的前n项和为Sn，已知a1＝2，S6＝22.

    (1)求Sn的表达式；

    (2)若从{an}中抽取一个公比为q的等比数列{akn}，其中k1＝1，且k1<k2<…<kn(kn∈N*)．

    ①当q取最小值时，求{kn}的通项公式；

    ②若关于n(n∈N*)的不等式6Sn>kn＋1有解，试求q的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A，B，C，其中A＝{a1，a2，…，an}，B＝{b1，b2，…，bn}，C＝{c1，c2，…，cn}，若A，B，C中的元素满足条件：c1＜c2＜…＜cn，ak＋bk＝ck(k＝1,2,3，…，n)，则称M为“完并集合”．

    (1)若M＝{1，x,3,4,5,6}为“完并集合”，则x的一个可能值为________．(写出一个即可)

    (2)对于“完并集合”M＝{1,2,3,4,5,6,7,8,9,10,11,12}，在所有符合条件的集合C中，其元素乘积最小的集合是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数是奇函数,当时, f(x)=x(1+x),则当时,f(x)= _____________

    查看答案和解析>>

    同步练习册答案