
| A. | y=sin$\frac{x}{2}$ | B. | y=2sinx | C. | y=sin4π | D. | y=sin(-4x) |
分析 找出解析式中ω的值,代入周期公式T=$\frac{2π}{|ω|}$,分别求出各项的最小正周期,即可作出判断.
解答 解:A、y=sin$\frac{x}{2}$,∵ω=$\frac{1}{2}$,∴T=$\frac{2π}{\frac{1}{2}}$=4π,本选项错误;
B、y=2sinx,∵ω=1,∴T=$\frac{2π}{1}$=2π,本选项错误;
C、y=sin4π=0,本选项错误;
D、y=sin(-4x)=-sin4x,∵ω=4,∴T=$\frac{2π}{4}$=$\frac{π}{2}$,本选项正确.
综上知,D选项正确.
故选:D.
点评 此题考查了三角函数的周期性及其求法,涉及的知识为正弦函数的周期性,熟练掌握周期公式是解本题的关键,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$π | B. | $\frac{3}{4}$π | C. | $\frac{5}{6}$π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-7=0 | B. | 2x-y-7=0 | C. | 2x+y+7=0 | D. | 2x-y+7=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 抽取人数 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
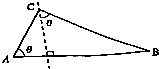 某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.
某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com