
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
分析 根据所给的数据完成列联表,求得观测值所用的数据,把数据代入观测值公式中,做出观测值χ2,同临界值表进行比较,χ2≈39.6>6.635,有99%的把握认为“桑葚毛虫皮炎与采桑”有关.
解答 解:完成2×2列联表:
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | 30 |
| 健康人数 | 5 | 78 | 83 |
| 合计 | 23 | 90 |
点评 本题考查独立性检验的应用,考查计算能力,属于基础题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | [-2,0) | C. | [-2,1] | D. | (-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
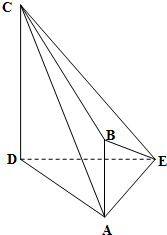 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=cosx | C. | y=tan$\frac{x}{2}$ | D. | y=cos4x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin$\frac{x}{2}$ | B. | y=2sinx | C. | y=sin4π | D. | y=sin(-4x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 3 | 2 | 1 | 0 |
| P | $\frac{1}{10}$ | b | $\frac{3}{10}$ | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com