
| X | 3 | 2 | 1 | 0 |
| P | $\frac{1}{10}$ | b | $\frac{3}{10}$ | a |
分析 (1)由分层抽样的性质,能求出抽取的5人中男、女同学的人数.
(2)由题意可得a=P(X=3)═,从而b=,由此能求出数学期望EX.
(3)由两组数据中相对应的数字之差均为10,得到${{s}_{1}}^{2}$=${{s}_{2}}^{2}$.
解答 解:(1)由分层抽样的性质得:
抽取的5人中男同学的人数为$\frac{5}{50}$×30=3,
女同学的人数为$\frac{5}{50}$×20=2.
(2)由题意可得:P(X=0)=$\frac{{2A}_{4}^{4}}{{A}_{5}^{5}}$=$\frac{2}{5}$.
即a=$\frac{2}{5}$,
因为a+b+$\frac{1}{10}$+$\frac{3}{10}$=1,
所以 b=$\frac{1}{5}$.
所以EX=3×$\frac{1}{10}$+2×$\frac{1}{5}$+1×$\frac{3}{10}$+0×$\frac{2}{5}$=1.
(3)${{s}_{1}}^{2}$=${{s}_{2}}^{2}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.


科目:高中数学 来源: 题型:解答题
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 抽取人数 | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
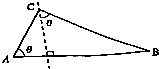 某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.
某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0和-4 | B. | 0;b取任意实数 | C. | 0和4 | D. | 4;b取任意实数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com