
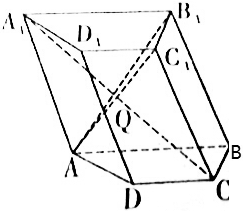
 体积为$\frac{9\sqrt{2}}{8}$的四棱柱ABCD-A1B1C1D1的底面为梯形,DC∥AB,AB=2AD=2DC=2,∠DAB=60°,平面DCC1D1⊥平面ABCD,且二面角A1-AD-C的余弦值为-$\frac{1}{3}$.
体积为$\frac{9\sqrt{2}}{8}$的四棱柱ABCD-A1B1C1D1的底面为梯形,DC∥AB,AB=2AD=2DC=2,∠DAB=60°,平面DCC1D1⊥平面ABCD,且二面角A1-AD-C的余弦值为-$\frac{1}{3}$.分析 (I)如图所示,过点D作DO⊥AB,垂足为O,过点C作CE⊥AB,垂足为E.在Rt△ADO中,∠DAB=60°,可得AO=$\frac{1}{2}$AD=$\frac{1}{2}$,DO=$\frac{\sqrt{3}}{2}$,四边形DCEO是矩形,可得梯形ABCD是等腰梯形.过点O作OM⊥A1B1,垂足为M,利用面面垂直的性质定理可得OM⊥平面ABCD.可得:$\frac{9\sqrt{2}}{8}$=OM×S梯形ABCD=OM×$\frac{3\sqrt{3}}{4}$.解得OM=$\frac{\sqrt{6}}{3}$.
如图所示,建立空间直角坐标系.设A1$(0,t,\frac{\sqrt{6}}{3})$,设平面DAA1D1的法向量为$\overrightarrow{m}$=(x,y,z),利用$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=0}\\{\overrightarrow{m}•\overrightarrow{A{A}_{1}}=0}\end{array}\right.$,可得$\overrightarrow{m}$,取平面ABCD的法向量为$\overrightarrow{n}$=(0,0,1),利用|$cos<\overrightarrow{m},\overrightarrow{n}>$|=$\frac{\overrightarrow{|m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{3}$,解得t.设D1$(\frac{\sqrt{3}}{2},s,\frac{\sqrt{6}}{3})$,利用$\overrightarrow{D{D}_{1}}$•$\overrightarrow{m}$=0,解得s,可得C1.利用cos$<\overrightarrow{A{C}_{1}},\overrightarrow{BC}>$=$\frac{\overrightarrow{A{C}_{1}}•\overrightarrow{BC}}{|\overrightarrow{A{C}_{1}}||\overrightarrow{BC}|}$,可得tan$<\overrightarrow{A{C}_{1}},\overrightarrow{BC}>$.
(II)连接A1B,交AB1于点P,连接PQ,由BC∥B1C1,可得BC∥平面AB1C1,BC∥PQ,由点P是A1C的中点,可得点Q是A1C的中点.求出$\overrightarrow{{A}_{1}C}$,即可得出.
解答 解:(I)如图所示,过点D作DO⊥AB,垂足为O,过点C作CE⊥AB,垂足为E.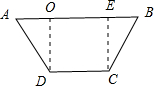

在Rt△ADO中,∠DAB=60°,
∴AO=$\frac{1}{2}$AD=$\frac{1}{2}$,DO=$\frac{\sqrt{3}}{2}$.
四边形DCEO是矩形,OE=DC=1,
∴BE=$\frac{1}{2}$,CB=$\sqrt{B{E}^{2}+E{C}^{2}}$=1.
∴梯形ABCD是等腰梯形.
S梯形ABCD=$\frac{(1+2)×\frac{\sqrt{3}}{2}}{2}$=$\frac{3\sqrt{3}}{4}$.
过点O作OM⊥A1B1,垂足为M,
∵平面DCC1D1⊥平面ABCD,
∴OM⊥平面ABCD.
由已知可得:$\frac{9\sqrt{2}}{8}$=OM×S梯形ABCD=OM×$\frac{3\sqrt{3}}{4}$.
解得OM=$\frac{\sqrt{6}}{3}$.
如图所示,建立空间直角坐标系.
O(0,0,0),A(0,-$\frac{1}{2}$,0),D$(\frac{\sqrt{3}}{2},0,0)$,C$(\frac{\sqrt{3}}{2},1,0)$,M$(0,0,\frac{\sqrt{6}}{3})$,A1$(0,t,\frac{\sqrt{6}}{3})$,
C$(\frac{\sqrt{3}}{2},1,0)$,B$(0,\frac{3}{2},0)$,
$\overrightarrow{AD}$=$(\frac{\sqrt{3}}{2},\frac{1}{2},0)$,$\overrightarrow{A{A}_{1}}$=$(0,t+\frac{1}{2},\frac{\sqrt{6}}{3})$.
设平面DAA1D1的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=0}\\{\overrightarrow{m}•\overrightarrow{A{A}_{1}}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}x+\frac{1}{2}y=0}\\{(t+\frac{1}{2})y+\frac{\sqrt{6}}{3}z=0}\end{array}\right.$,
取$\overrightarrow{m}$=$(1,-\sqrt{3},\frac{3\sqrt{2}(2t+1)}{4})$,
取平面ABCD的法向量为$\overrightarrow{n}$=(0,0,1),
则|$cos<\overrightarrow{m},\overrightarrow{n}>$|=$\frac{\overrightarrow{|m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{|\frac{3\sqrt{2}(2t+1)}{4}|}{\sqrt{4+\frac{9(2t+1)^{2}}{8}}}$=$\frac{1}{3}$,
化为(2t+1)2=$\frac{4}{9}$,
解得t=-$\frac{1}{6}$,或t=-$\frac{5}{6}$.
取t=-$\frac{5}{6}$.
设D1$(\frac{\sqrt{3}}{2},s,\frac{\sqrt{6}}{3})$,$\overrightarrow{D{D}_{1}}$=$(0,s,\frac{\sqrt{6}}{3})$,
∵$\overrightarrow{D{D}_{1}}$⊥$\overrightarrow{m}$,
∴$\overrightarrow{D{D}_{1}}$•$\overrightarrow{m}$=$-\sqrt{3}s$-$\frac{\sqrt{3}}{3}$=0,
解得s=$-\frac{1}{3}$,
∴C1$(\frac{\sqrt{3}}{2},\frac{2}{3},\frac{\sqrt{6}}{3})$.
$\overrightarrow{A{C}_{1}}$=$(\frac{\sqrt{3}}{2},\frac{7}{6},\frac{\sqrt{6}}{3})$,$\overrightarrow{BC}$=$(\frac{\sqrt{3}}{2},-\frac{1}{2},0)$.
cos$<\overrightarrow{A{C}_{1}},\overrightarrow{BC}>$=$\frac{\overrightarrow{A{C}_{1}}•\overrightarrow{BC}}{|\overrightarrow{A{C}_{1}}||\overrightarrow{BC}|}$=$\frac{\frac{1}{6}}{\sqrt{\frac{25}{9}}×\sqrt{\frac{3}{4}+\frac{1}{4}}}$=$\frac{1}{10}$,
∴tan$<\overrightarrow{A{C}_{1}},\overrightarrow{BC}>$=$\sqrt{99}$=3$\sqrt{11}$.
(II)连接A1B,交AB1于点P,连接PQ,
∵BC∥B1C1,BC?平面AB1C1,B1C1?平面AB1C1,
∴BC∥平面AB1C1,
平面A1BC∩平面AB1C1=PQ,
∴BC∥PQ,
∵点P是A1C的中点,
∴点Q是A1C的中点.
∵$\overrightarrow{{A}_{1}C}$=$(\frac{\sqrt{3}}{2},\frac{11}{6},-\frac{\sqrt{6}}{3})$,
∴$|\overrightarrow{{A}_{1}C}|$=$\sqrt{(\frac{\sqrt{3}}{2})^{2}+(\frac{11}{6})^{2}+(-\frac{\sqrt{6}}{3})^{2}}$=$\frac{\sqrt{43}}{3}$.
∴$|\overrightarrow{{A}_{1}Q}|$=$\frac{1}{2}$$|\overrightarrow{{A}_{1}C}|$=$\frac{\sqrt{43}}{6}$.
点评 本题考查了空间位置关系及其空间角、线面面面平行垂直的判定与性质定理、等腰梯形、直角三角形的边角关系、三角形中位线定理,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
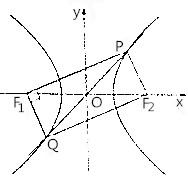 如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )
如图,F1,F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右两个焦点.若直线y=x与双曲线C交于P、Q两点,且四边形PF1QF2为矩形,则双曲线的离心率为( )| A. | 2+$\sqrt{2}$ | B. | 2+$\sqrt{6}$ | C. | $\sqrt{2+\sqrt{2}}$ | D. | $\sqrt{2+\sqrt{6}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
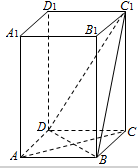 如图,ABCD-A1B1C1D1是正四棱柱.
如图,ABCD-A1B1C1D1是正四棱柱.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (-1,6) | C. | (1,3) | D. | (3,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com