
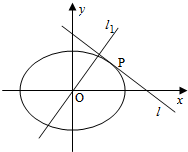
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.分析 (1)由题意得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{2ab=4\sqrt{3}}\end{array}\right.$,从而解得椭圆C的方程.
(2)设直线l的方程为y=kx+m(k<0),从而由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$可得点P($\frac{-4k}{\sqrt{3+4{k}^{2}}}$,$\frac{3}{\sqrt{3+4{k}^{2}}}$),再写出直线l1的方程为x+ky=0,从而化简点P到直线l1的距离d=$\frac{1}{\sqrt{7+4{k}^{2}+\frac{3}{{k}^{2}}}}$,由基本不等式可得4k2+$\frac{3}{{k}^{2}}$≥2$\sqrt{12}$=4$\sqrt{3}$,从而求最大值即可.
解答 解:(1)由题意得,
$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\\{2ab=4\sqrt{3}}\end{array}\right.$,
解得,a=2,b=$\sqrt{3}$;
故椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.
(2)设直线l的方程为y=kx+m(k<0),
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$消去y得,
(3+4k2)x2+8kmx+4m2-12=0.
由天直线l与椭圆C只有一个公共点,
故△=0,化简得3-m2+4k2=0,
解得点P(-$\frac{4km}{3+4{k}^{2}}$,$\frac{3m}{3+4{k}^{2}}$),
又点P在第一象限,故点P($\frac{-4k}{\sqrt{3+4{k}^{2}}}$,$\frac{3}{\sqrt{3+4{k}^{2}}}$),
∵过原点O的直线l1与l垂直,
∴直线l1的方程为x+ky=0,
∴点P到直线l1的距离d=$\frac{|\frac{-4k}{\sqrt{3+4{k}^{2}}}+\frac{3k}{\sqrt{3+4{k}^{2}}}|}{\sqrt{1+{k}^{2}}}$=$\frac{1}{\sqrt{7+4{k}^{2}+\frac{3}{{k}^{2}}}}$,
∵4k2+$\frac{3}{{k}^{2}}$≥2$\sqrt{12}$=4$\sqrt{3}$(当且仅当k2=$\frac{\sqrt{3}}{2}$时,等号成立),
∴$\frac{1}{\sqrt{7+4{k}^{2}+\frac{3}{{k}^{2}}}}$≤$\frac{1}{\sqrt{7+4\sqrt{3}}}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$.
故点P到直线l1的距离的最大值为2-$\sqrt{3}$.
点评 本题考查了圆锥曲线的标准方程的求法,直线与圆锥曲线的综合应用,基本不等式的应用,同时考查了学生的化简运算的能力,属于难题.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{2\;013}{2\;015}$ | B. | $\frac{2\;013}{2\;014}$ | C. | $\frac{2\;012}{2\;013}$ | D. | $\frac{2\;011}{2\;012}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)的图象关于点(-$\frac{π}{3}$,0)中心对称 | B. | y=g(x)的图象关于x=-$\frac{π}{6}$轴对称 | ||
| C. | y=g(x)在区间[-$\frac{5π}{12}$,-$\frac{π}{6}$]单调递增 | D. | y=g(x)在[-$\frac{π}{6}$,$\frac{π}{3}$]单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | (?p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0.50] | (0,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
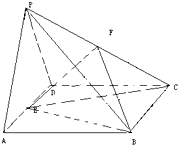 如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,
如图,△PAD为边长为2的等边三角形,ABCD为菱形,∠DAB=60°,E为AD的中点,平面PAD⊥平面ABCD,F为棱PC上一点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com