
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康.经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加.为了制定提升农民年收入、实现2020年脱贫的工作计划,该地扶贫办统计了2019年50位农民的年收入并制成如下频率分布直方图:

(1)根据频率分布直方图,估计50位农民的年平均收入![]() 元(单位:千元)(同一组数据用该组数据区间的中点值表示);
元(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入X服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() ,利用该正态分布,求:
,利用该正态分布,求:
(i)在扶贫攻坚工作中,若使该地区约有占总农民人数的84.14%的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况,扶贫办随机走访了1000位农民.若每位农民的年收入互相独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附参考数据:![]() ,若随机变量X服从正态分布
,若随机变量X服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(1)17.40千元;(2)(i)14.77千元.(ii)978人.
【解析】
(1)求解每一组数据的组中值与频率的乘积,将结果相加即可得到对应的![]() ;
;
(2)(i)根据![]() 的数值判断出年收入的取值范围,从而可计算出最低年收入;
的数值判断出年收入的取值范围,从而可计算出最低年收入;
(ii)根据![]() 的数值判断出每个农民年收入不少于
的数值判断出每个农民年收入不少于![]() 千元的概率,然后根据二项分布的概率计算公式计算出“恰有
千元的概率,然后根据二项分布的概率计算公式计算出“恰有![]() 个农民年收入不少于
个农民年收入不少于![]() ”中
”中![]() 的最大值即可.
的最大值即可.
解:(1)![]() 千元
千元
故估计50位农民的年平均收入![]() 为17.40千元;
为17.40千元;
(2)由题意知![]()
(i)![]() ,
,
所以![]() 时,满足题意,
时,满足题意,
即最低年收入大约为14.77千元.
(ii)由![]() ,
,
每个农民的年收入不少于12.14千元的事件的概率为0.9773,
记1000个农民的年收入不少于12.14千元的人数为![]() ,
,
则![]() ,其中
,其中![]() ,
,
于是恰好有k个农民的年收入不少于12.14千元的事件概率为![]() ,
,
从而由![]()
得![]() ,而
,而![]() ,
,
所以,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
由此可知,在所走访的1000位农民中,年收入不少于12.14千元的人数最有可能是978人.


科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
, ![]() ,
,
![]() ,
, ![]()
(1).求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2).判断变量![]() 与
与![]() 之间的正相关还是负相关;
之间的正相关还是负相关;
(3).若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘估计公式分别为
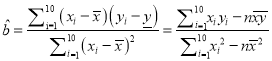
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法:
①残差点分布的带状区域的宽度越窄相关指数越小
②在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加
平均增加![]() 个单位;
个单位;
④对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是![]()
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题,其中错误命题的个数为( )
(1)直线![]() 与平面
与平面![]() 不平行,则
不平行,则![]() 与平面
与平面![]() 内的所有直线都不平行;
内的所有直线都不平行;
(2)直线![]() 与平面
与平面![]() 不垂直,则
不垂直,则![]() 与平面
与平面![]() 内的所有直线都不垂直;
内的所有直线都不垂直;
(3)异面直线![]() 、
、![]() 不垂直,则过
不垂直,则过![]() 的任何平面与
的任何平面与![]() 都不垂直;
都不垂直;
(4)若直线![]() 和
和![]() 共面,直线
共面,直线![]() 和
和![]() 共面,则
共面,则![]() 和
和![]() 共面
共面
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),直
为参数),直![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)当![]() 时,直线
时,直线![]() 与
与![]() 相交于
相交于![]() 两点;过点
两点;过点![]() 作
作![]() 的垂线
的垂线![]() ,
,![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个平行于圆锥底面的平面去截圆锥,截得圆台的母线长为![]() ,两底面面积分别为
,两底面面积分别为![]() 和
和![]() .求:
.求:
(1)圆台的高;
(2)圆台的体积;
(3)截得此圆台的圆锥的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)若函数![]() 在区间
在区间![]() 上不是单调函数,求实数
上不是单调函数,求实数![]() 的取值范围;
的取值范围;
(II)是否存在实数![]() ,使得函数
,使得函数![]() 图像与直线
图像与直线![]() 有两个交点?若存在,求出所有
有两个交点?若存在,求出所有![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com