
分析 (1)由f(0)=0求出k的值,分离参数得到t>2sinθ+2cosθ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),根据三角形函数的性质即可求出t范围.
(2)由f(1)=$\frac{3}{2}$,可解得a=2,于是可得f(x)=2x-2-x,g(x)=22x+2-2x-2m(2x-2-x),令t=2x-2-x,则g(x)=h(t)=t2-2mt+2=(t-m)2+2-m2,t∈[$\frac{3}{2}$,+∞),通过对m范围的讨论,结合题意h(t)min=-1,即可求得m的值
解答 解:(1)∵函数f(x)=ax-(k-1)a-x(a>0且a≠1)是定义域为R的奇函数.
∴f(0)=0,
∴1-(k-1)=0,
解得k=2,
∴f(x)=ax-a-x,
∵f(1)=a-$\frac{1}{a}$>0,且a>0且a≠1,
∴a>1,
∴f(x)是定义域为R的奇函数且单调递增,
∵f(sin2θ+cos2θ)+f(1-tcosθ)<0对所有的θ∈(0,$\frac{π}{2}$)均成立,
∴sin2θ+cos2θ+1-tcosθ<0,
即tcosθ>sin2θ+cos2θ+1=2sinθcosθ+2cos2θ,
∵θ∈(0,$\frac{π}{2}$),
∴cosθ∈(0,1),
则t>2sinθ+2cosθ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),
又当θ=$\frac{π}{4}$时,2$\sqrt{2}$sin(θ+$\frac{π}{4}$)的最大值为2$\sqrt{2}$,
∴t>2$\sqrt{2}$,
∴t的取值范围为(2$\sqrt{2}$,+∞);
(Ⅱ)由(1)知,f(x)=ax-a-x,
∵f(1)=$\frac{3}{2}$,
∴a-$\frac{1}{a}$=$\frac{3}{2}$,解得a=2.
故f(x)=2x-2-x,g(x)=22x+2-2x-2m(2x-2-x),
令t=2x-2-x,则22x+2-2x=t2+2,由x∈[1,+∞),得t∈[$\frac{3}{2}$,+∞),
∴g(x)=h(t)=t2-2mt+2=(t-m)2+2-m2,t∈[$\frac{3}{2}$,+∞),
当m≥$\frac{3}{2}$时,当t=m时,h(t)min=2-m2=-1,解得m=$\sqrt{3}$,或m=$-\sqrt{3}$(舍去),
当m<$\frac{3}{2}$时,当t=$\frac{3}{2}$,h(t)min=$\frac{17}{4}$-3m=1,解得m=$\frac{7}{4}$(舍去).
综上,m的值是2,$\sqrt{3}$.
点评 本题考查指数函数的综合应用,考查函数的奇偶性与单调性,函数恒成立的问题,突出换元思想与分类讨论思想在最值中的综合应用,属于难题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
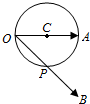 如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.
如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 最高气温x(℃) | 10 | 4 | -2 | -8 |
| 用电量y(度) | 20 | 44 | 56 | 80 |
| A. | 32度 | B. | 34度 | C. | 36度 | D. | 38度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com