
分析 (Ⅰ)利用诱导公式、和差化积公式、积化和差公式进行计算得到f(x)=$\sqrt{2}$sin(x+$\frac{π}{4}$),据此求得其最小正周期和单调区间;
(Ⅱ)利用(Ⅰ)的结论得到$\sqrt{2}sin({A+\frac{π}{4}})=\sqrt{2}$,易得A=$\frac{π}{4}$.由正弦定理得到:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}}{2}$.结合角B的取值范围和特殊角的三角函数值推知角B的大小,利用三角形内角和定理可以求得角C的大小,所以由余弦定理来求c的值即可.
解答 解:(Ⅰ)f(x)=sinx+sin(x+$\frac{π}{6}$)-cos(x+$\frac{4π}{3}$),
=sinx+$\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx-(-$\frac{1}{2}$)cosx+(-$\frac{\sqrt{3}}{2}$)sinx,
=sinx+cosx,
=$\sqrt{2}$sin(x+$\frac{π}{4}$),
∴f(x)的最小正周期T=2π.
由2kπ+$\frac{π}{2}$≤x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$(k∈Z),得
2kπ+$\frac{π}{4}$≤x≤2kπ+$\frac{5π}{4}$(k∈Z),故f(x)的单调递减区间是[2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$](k∈Z);
(Ⅱ)∵在锐角△ABC中,f(A)=$\sqrt{2}$,
∴$\sqrt{2}sin({A+\frac{π}{4}})=\sqrt{2}$,即sin(A+$\frac{π}{4}$)=1.由0≤A≤$\frac{π}{2}$,得A=$\frac{π}{4}$.
∵a=2,b=$\sqrt{6}$,
∴由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$,得sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{3}}{2}$.
由0≤B≤$\frac{π}{2}$,得B=$\frac{π}{3}$.故C=π-A-B=π-$\frac{π}{4}$-$\frac{π}{3}$=$\frac{5π}{12}$.
由余弦定理,c2=a2+b2-2abcosC=4+6-2×2×$\sqrt{6}$cos$\frac{5π}{12}$=10-4$\sqrt{6}$×$\frac{\sqrt{6}-\sqrt{2}}{4}$=4+2$\sqrt{3}$,
故c=$\sqrt{3}$+1.
点评 本题考查了正弦定理、余弦定理,三角函数的周期性和单调性,函数y=Asin(ωx+φ),x∈R及函数y=Acos(ωx+φ);x∈R(其中A、ω、φ为常数,且A≠0,ω>0)的周期T=2π÷ω.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=-3或a=2 | B. | a=-3 | C. | a=-2 | D. | a=3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
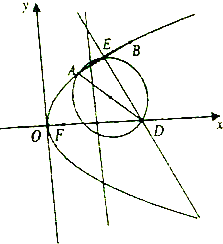 已知F(1,0)是抛物线y2=2px(p>0)的焦点.
已知F(1,0)是抛物线y2=2px(p>0)的焦点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com