证明:(1)∵a
n+1=f(a
n)=
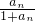
,所以
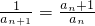
=
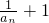
,
即
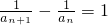
∴{

}是以2为首项,1为公差的等差数列,
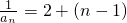
,即
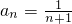
.(3分)
(2)∵a
n+1≤f(a
n)=
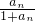
,a
n>0,
∴
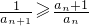
,即
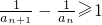
,
当n≥2时
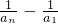
=
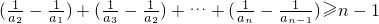
∴
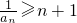
∴

.
当n=1时,上式也成立,
∴

,(n∈N
*)
∴b
n=
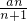
≤
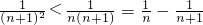
,
∴b
1+b
2+…+b
n<
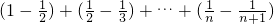
=1
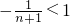
.(8分)
(3)∵a
1=

,a
2=g(a
1)=

,a
2-a
1=

-

=

>0.
又∵a
n+1-a
n=
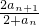
-
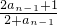
=
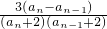
,
由迭代关系可知,a
n+1-a
n>0,∴a
n≥a
1=

.
又∵(2+a
n)(2+a
n-1)=(2+
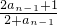
)(2+a
n-1)=5+4a
n-1≥7,
∴
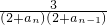
≤

,
∴|a
n+1-a
n|=
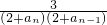
|a
n-a
n-1|≤

|a
n-a
n-1|,
∴|a
n+1-a
n|≤

|a
n-a
n-1|≤(

)
2|a
n-1-a
n-2|≤…≤(

)
n-1|a
2-a
1|=

(

)
n-1.(13分)
分析:(1)利用a
n+1=f(a
n)(n∈N
*),推出a
n+1与a
n的关系,然后推出{

}是等差数列,并求数列{a
n}的通项公式;
(2)通过a
n+1≤f(a
n)(n∈N
*),推出

,利用b
n=
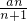
,放大b
n,然后通过求和b
1+b
2+…+b
n证明结论.
(3)由题意推出a
2-a
1>0.证明a
n+1-a
n>0,数列是递增数列,推出|a
n+1-a
n|与|a
n-a
n-1|的关系,通过放缩法证明即可.
点评:本题考查放缩法的应用,等差关系的确定,数列与不等式的综合应用,考查分析问题解决问题的能力,转化思想的应用.

 ,函数f(x)=
,函数f(x)= ,g(x)=
,g(x)=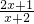 .
. }是等差数列,并求数列{an}的通项公式;
}是等差数列,并求数列{an}的通项公式;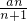 ,证明:b1+b2+…+bn<1;
,证明:b1+b2+…+bn<1; •(
•( )n-1.
)n-1.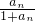 ,所以
,所以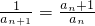 =
=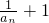 ,
,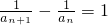
 }是以2为首项,1为公差的等差数列,
}是以2为首项,1为公差的等差数列,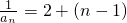 ,即
,即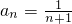 .(3分)
.(3分)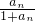 ,an>0,
,an>0,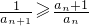 ,即
,即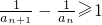 ,
,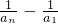 =
=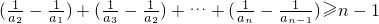
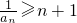
 .
. ,(n∈N*)
,(n∈N*)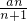 ≤
≤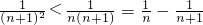 ,
,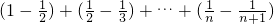 =1
=1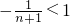 .(8分)
.(8分) ,a2=g(a1)=
,a2=g(a1)= ,a2-a1=
,a2-a1= -
- =
= >0.
>0.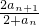 -
-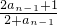 =
=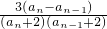 ,
, .
.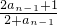 )(2+an-1)=5+4an-1≥7,
)(2+an-1)=5+4an-1≥7,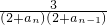 ≤
≤ ,
,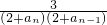 |an-an-1|≤
|an-an-1|≤ |an-an-1|,
|an-an-1|, |an-an-1|≤(
|an-an-1|≤( )2|an-1-an-2|≤…≤(
)2|an-1-an-2|≤…≤( )n-1|a2-a1|=
)n-1|a2-a1|= (
( )n-1.(13分)
)n-1.(13分) }是等差数列,并求数列{an}的通项公式;
}是等差数列,并求数列{an}的通项公式; ,利用bn=
,利用bn=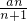 ,放大bn,然后通过求和b1+b2+…+bn证明结论.
,放大bn,然后通过求和b1+b2+…+bn证明结论.
