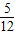已知圆C的方程为:x2+y2+2x-4y-20=0,
(1)若直线l1过点A(2,-2)且与圆C相切,求直线l1的方程;
(2)若直线l2过点B(-4,0)且与圆C相交所得的弦长为8,求直线l2的方程.
【答案】
分析:(1)先判断点A位置,因为A点满足圆方程,所以A点在圆上,则圆心与A点连线垂直于切线,只需求出圆心与A点连线的斜率,切线斜率就可求出,再用点斜式写出方程即可.
(2)在圆中,半径,半弦,弦心距构成直角三角形,因为圆的半径和半弦已知,利用勾股定理就可求出圆心到直线l
2的距离,再分斜率存在和不存在两种情况设出直线l
2的方程,利用点到直线的距离公式,求出参数的值,就可得到直线l
2的方程.
解答:解:圆C的方程化为:(x+1)
2+(y-2)
2=25,圆心C(-1,2),半径r=5,
(1)易知A(2,-2)在圆C上,则l
1⊥AC,可求得k
AC=-

,∴
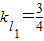
;
则直线l
1的方程为:y+2=

(x-2).即3x-4y-14=0
(2)设圆心到直线l
2的距离为d,
∵弦长为8,又圆的半径r=5,∴d=3
①若l
2斜率不存在,∵过点B(-4,0),即l
2方程为x=-4,
此时 圆心C(-1,2)到l
2的距离为3,所以方程x=-4符合题意;
②若l
2斜率存在,∵过点B(-4,0),
设l
2方程为y=k(x+4),即kx-y+4k=0,
∵圆心C(-1,2)到l
2的距离为3,
∴

=3,解得k=-
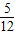
此时l
2方程为:5x+12y+20=0
综上得直线l
2方程为:x+4=0或5x+12y+20=0;
点评:本题主要考查了已知切点坐标求切线方程,圆的几何性质的应用,以及点到直线的距离公式的应用.属于综合题.

 ,∴
,∴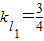 ;
; (x-2).即3x-4y-14=0
(x-2).即3x-4y-14=0  =3,解得k=-
=3,解得k=-