
���� �����a+bԪ�����������ȴ�A���ش���ȷ����ѡ���B������Ҳ��ȷ���ɴ������ǡ�û�ý���a+bԪ�ĸ��ʣ�
�������Ȼش�Aʱ��õĽ�����Ϊ��Ԫ���Ȼش�Bʱ��õĽ�����Ϊ��Ԫ���ֱ������ѧ�������ɴ�����������
��� �⣺�����a+bԪ���������ǣ�
�ȴ�A���ش���ȷ����ѡ���B������Ҳ��ȷ��
��ǡ�û�ý���a+bԪ�ĸ���P=$\frac{1}{3}��\frac{1}{2}��\frac{1}{4}$=$\frac{1}{24}$��
�������Ȼش�Aʱ��õĽ�����Ϊ��Ԫ��
�εķֲ���Ϊ��
| �� | 0 | $\frac{a}{2}$ | a | a+b |
| P | $\frac{2}{3}$ | $\frac{1}{8}$ | $\frac{1}{6}$ | $\frac{1}{24}$ |
| �� | 0 | $\frac{b}{2}$ | b | a+b |
| P | $\frac{3}{4}$ | $\frac{1}{12}$ | $\frac{1}{8}$ | $\frac{1}{24}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��С���ѧ��������Ӧ�ã����е��⣬����ʱҪ�������⣬������߿��ж��DZؿ�����֮һ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
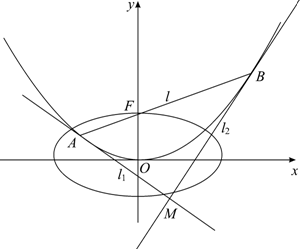 ��֪������C��x2=4y�Ľ���ΪF������F��ֱ��l��������C��A��B���㣻��ԲE��������ԭ�㣬������x���ϣ���F������һ�����㣬����������e=$\frac{{\sqrt{3}}}{2}$��
��֪������C��x2=4y�Ľ���ΪF������F��ֱ��l��������C��A��B���㣻��ԲE��������ԭ�㣬������x���ϣ���F������һ�����㣬����������e=$\frac{{\sqrt{3}}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
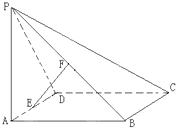 ��ͼ������P-ABCD�ĵ�����ƽ���ı��Σ���DAB=60�㣬ƽ��PAB��ABD��
��ͼ������P-ABCD�ĵ�����ƽ���ı��Σ���DAB=60�㣬ƽ��PAB��ABD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{5}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
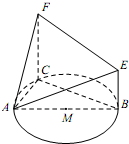 ��ͼ��ij�������һ����ABC�ڽ���ԲM��AB��ԲM��ֱ����CF��BE��BE��ƽ��ABC����AB=2��AC=1��BE+CF=7��
��ͼ��ij�������һ����ABC�ڽ���ԲM��AB��ԲM��ֱ����CF��BE��BE��ƽ��ABC����AB=2��AC=1��BE+CF=7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��0�� | B�� | ��0��-1�� | C�� | ��-$\frac{1}{16}$��0�� | D�� | ��0��-$\frac{1}{16}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����̥ | ������̥ | �ϼ� | |
| 70�� | 30 | 15 | 45 |
| 80�� | 45 | 10 | 55 |
| �ϼ� | 75 | 25 | 100 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com