
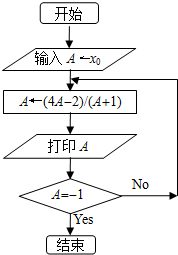
 若根据如图的框图,产生数列{an}.
若根据如图的框图,产生数列{an}.分析 (1)根据程序中各变量、各语句的作用,计算x0=$\frac{49}{65}$时输出的A值即可;
(2)根据程序中的计算公式得an+1=$\frac{{4a}_{n}-2}{{a}_{n}+1}$,an+1=an=x0,列出方程求出x0的值即可.
解答 解:(1)根据程序中各变量、各语句的作用知:
当x0=$\frac{49}{65}$时,计算并输出a1=$\frac{4×\frac{49}{65}-2}{\frac{49}{65}+1}$=$\frac{11}{19}$,
a2=$\frac{4×\frac{11}{19}-2}{\frac{11}{19}+1}$=$\frac{1}{5}$,
a3=$\frac{4×\frac{1}{5}-2}{\frac{1}{5}+1}$=-1,
结束程序;(3分)
(2)根据程序中的计算公式,得
an+1=$\frac{{4a}_{n}-2}{{a}_{n}+1}$,
令an+1=an=x0,
则$\frac{{4x}_{0}-2}{{x}_{0}+1}$=x0,
解得x0=1或x0=2,
此时执行程序将产生一个无穷常数列.(8分)
点评 本题利用程序框图考查了数列与递推公式的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
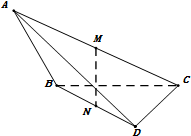 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 销售额(x)/万元 | 3 | 5 | 6 | 7 | 9 |
| 利润额(y)/万元 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com