
分析 (Ⅰ)由曲线C的极坐标方程能求出曲线C的直角坐标方程;直线l的参数方程消去t,能求出直线l的普通方程.
(Ⅱ)点P(0,$\sqrt{3}$)在直线l:$\sqrt{3}x+y=\sqrt{3}$上,将直线l的参数方程代入曲线C的直角坐标方程,得5t2+12t-4=0,设两根为t1,t2,则${t}_{1}+{t}_{2}=-\frac{12}{5}$,${t}_{1}{t}_{2}=-\frac{4}{5}$,由此能求出$\frac{1}{|PA|}$+$\frac{1}{|PB|}$.
解答 解:(Ⅰ)∵曲线C的极坐标方程为${ρ^2}=\frac{4}{{1+{{cos}^2}θ}}$,
∴曲线C的直角坐标方程为$\frac{{x}^{2}}{2}+\frac{{y}^{2}}{4}=1$,
∵直线l的参数方程为$\left\{{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=\sqrt{3}+\frac{{\sqrt{3}}}{2}t}\end{array}}\right.(t$为参数),
∴消去t得直线l的普通方程为$\sqrt{3}x+y=\sqrt{3}$.…(5分)
(Ⅱ)点P(0,$\sqrt{3}$)在直线l:$\sqrt{3}x+y=\sqrt{3}$上,将直线l的参数方程代入曲线C的直角坐标方程,
得2(-$\frac{1}{2}t$)2+($\sqrt{3}+\frac{\sqrt{3}}{2}t$)2=4,∴5t2+12t-4=0,
设两根为t1,t2,则${t}_{1}+{t}_{2}=-\frac{12}{5}$,${t}_{1}{t}_{2}=-\frac{4}{5}$,故t1与t2异号,
∴|PA|+|PB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\frac{4\sqrt{14}}{5}$,
|PA|•|PB|=|t1•t2|=-t1t2=$\frac{4}{5}$,
∴$\frac{1}{|PA|}$+$\frac{1}{|PB|}$=$\frac{|PA|+|PB|}{|PA|•|PB|}$=$\sqrt{14}$.…(10分)
点评 本题考查曲线的直角坐标方程及直线的普通方程的求法,考查两线段倒数和的取值范围的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N=U | B. | (∁UM)∪(∁UN)=U | C. | M∩(∁UN)=∅ | D. | (∁UM)∪(∁UN)=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
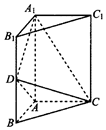 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com